Экономические науки/8.Математические методы в экономике.

Павлова М.Г., Нестеренко Ю.Ю.

Автомобільно- дорожній інститут ДВНЗ „Донецький національний технічний університет”

БЛОЧНІ ЗАДАЧІ ЛІНІЙНОГО ПРОГРАМУВАННЯ. МЕТОД ДАНЦІГА-ВУЛФА

При розв’язанні задач планування та оперативного управління в економічних системах доцільно використовувати принцип декомпозиції, який полягає у роздрібненні основної задачі великої розмірності на підзадачі меншої розмірності, знаходження незалежних розв’язків для кожної з них та наступного об’єднання цих розв’язків в одне загальне рішення вихідної задачі. Також при рішенні таких задач необхідно враховувати умову цілочисельності використовуваних змінних.

Постановка задач даного класу відноситься до виробничих комплексів, холдінгів, фінансово-промисловим групам, корпораціям и т.д. В свою чергу, вони мають в своєму складі декілька інших підприємств, що відрізняються своїми індивідуальними локальними характеристиками (ресурси, показники), але в той же час об’єднаних сукупністю обмежень(загальними для усієї системи) та однієї цільової функції.

Сучасні програмні засоби в більшості випадків використовують спеціальні методи рішення з декомпозицією задачі на під задачі, наприклад метод декомпозиції Данцига-Вулфа,за цим методом кожний блок матриці формується та розглядається автономно, як окрема підзадача з наступним об’єднанням на етапі остаточної постанови задачі. Такі задачі економічно інтерпретуються як задачі багаторівневої ієрархічної структури.

Методи розв’язування задач великої розмірності ґрунтуються на вивченні структури матриці обмежень та мають вигляд матриці блочно-діагональної структури, такої як:

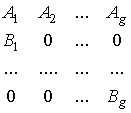
де А_i, B_j – підматриці [2].

Загалом, задачу великої розмірності можна представити наступним чином: до складу фірми, що випускає певні вироби, входить g відділень, кожне з яких для виробництва використовує незалежні від інших відділень автономні ресурси (для і-го відділення норми витрат незалежних ресурсів відображаються підматрицею В_і). Окрім того, в розпорядженні керівництва фірми є спільні ресурси, норми витрати яких задані зв’язуючи рядком [A₁, A₂, …, A_g] матриці обмежень. Необхідно побудувати такий план виробництва, для якого б досягався максимальний прибуток фірми загалом [1].

Відповідна задача ЛП має вигляд:

Q=c₁x₁+c₂x₂+…+c_gx_g ® Max

A₁x₁+A₂x₂+…+A_gx_g=b₀

B₁x₁ =b₁

B₂x₂ =b₁

……

B_gx_g =b_g

Де с_j – прибуток від реалізації одиниці j–го продукту;

x_j – кількість продукції j–го типу, яка випускається;

Q – прибуток від реалізації продукції;

A_j – норми витрат ресурсів фірми;

B_j – норми витрат незалежних ресурсів.

Так як множини R_j={x: B_jx_j=b_j; x_j≥0}, - непусті та обмежені, а , k=1,…K_j – екстремальні точки цієї множини, будь-яка з точок множини R_j може бути представленою у вигляді опуклої комбінації крайніх точок, тобто. Підставивши отримані співвідношення у первісну задачу отримуємо:

………

Ця задача є головною – координуючою задачею. Розв’язок задачі – це знаходження невідомих значень . Оптимальний розв’язок знаходиться за допомогою дворівневої процедури, яка має назву методу Данціга-Вулфа. У цьому методі не зберігаються всі стовпці матриці обмежень координуючої задачі – вони отримуються по мірі необхідності з використанням методу генерації стовпців та розв’язуванням множини допоміжних підзадач з використанням первісних матриць В_і[1].

Еквівалентна форма координуючої задачі має вигляд:

,,,

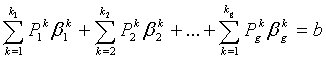
Де , .

Розв’язання цієї задачі відносно невідомих дозволяє знайти остаточний розв’язок, тому що _.

Останній етап розв’язання задачі великої розмірності реалізується за допомогою процедури генерації стовпчиків, за допомогою якої й отримують значення компоненту, що включається до бази.

Нехай В ‑ біжуча база, С_в ‑ вектор коефіцієнтів функції мети при базових змінних. Біжучий розв’язок є оптимальним, якщо для всіх небазових векторів виконується умова оптимальності , де згідно з визначенням координуючої задачі та , одиничний вектор має n компонент, одиниця знаходиться в (r₀+j)-ій позиції. Здійснимо наступні перетворення: нехай

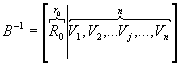, де R₀ – матриця (r₀ +n)r₀, що складається з перших r₀ стовпчиків матриці В^-1, а V_j – (r₀+j) –й стовпчик цієї ж матриці [3]. У цьому випадку

Якщо біжучий розв’язок неоптимальний, то вектор повинен бути включений до бази. Суттєвим є те, що не можна обчислити до тих пір, поки не відомі всі елементи , що є неможливим поки не відома відповідна кутова точка .

Щоб прискорити рішення, задачу можна звести до визначення кутової точкикожної з підмножин, яка має мінімальне значення . Нехай

, то

Таким чином, якщо , то змінна , що відповідає , повинна бути введена до бази. В іншому випадку, якщо, отриманий розв’язок є оптимальним [1].

Висновок. Процес розв’язку задач великої розмірності методом Данціга-Вулфа ітеративне повторюється до моменту отримання оптимального розв’язку задачі загалом, або ж до того моменту, коли будуть виконані умови зупинки. Декомпозиція полягає у роздрібненні вихідної задачі на під задачі значно меншої розмірності, що можуть бути розв’язані наявними засобами.

Література

1. Катренко А.В. Дослідження операцій. Підручник. – Львів: «Магнолія Плюс», 2004. – с.66-76, 105-110.

2. Зайченко Ю.П. Исследование операций. – К.: Вища школа, 1986. – с.45-61,66.

3. Дегтяров Ю.И. Исследование операций. – М.: Высшая школа,1986. – с.121-140.