T.R. Amanbayev* and S.J. Antony**
*Southern Kazakh State University,
Shymkent, Kazakhstan, E-mail: tulegen_amanbaev@mail.ru
**Institute of Particle Science and
Engineering, University of Leeds, Leeds, LS2 9JT, UK, E-mail: S.J.Antony@leeds.ac.uk
MODELING AND COMPUTATION OF THE LIFTING OF THE AIR BUBBLE TAKING INTO ACCOUNT
OF SURFACE MINERALIZATION
For enrichment of material by method of flotation
the alone fact of docking the hydrophobic particles on air bubbles is
insufficiently. The resulting system must rise to the surface of liquid
resulting the interaction with the hydrodynamic flows in the chamber of machines.
On this process influences the collisions and capture of other moving particles.
Occur in which the process of lifting of the "bubble-particles" complexes
to the liquid surface is one of the important stages of flotation, which is
modeled in the present work.
Consider the motion of a single bubble in
a fluid with mineralization of it’s surface (filled by particles). We assume that the shape of the bubble and
particles are spherical. Further the lower indices l, b and p of the parameters represent respectively
liquid, bubble and particle. The parameters of flotation complex are noted without
lower index.
The equations
of the motion. The mass balance’s equation of flotation complex has the form
![]() (1)
(1)
where ![]() - mass of flotation complex; t - time, j - intensity of capture of particles. Let us write the equation of
flotation complex’s motion for one-dimensional case (along X-axis against the
vector of acceleration of gravity). Then we have
- mass of flotation complex; t - time, j - intensity of capture of particles. Let us write the equation of
flotation complex’s motion for one-dimensional case (along X-axis against the
vector of acceleration of gravity). Then we have
![]() (2)
(2)
![]() ,
, ![]() ,
, 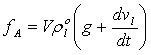
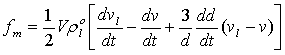 ,
, 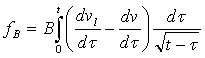 (3)
(3)
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Here ![]() - the velocity of flotation complex;
- the velocity of flotation complex; ![]() - the characteristic velocity of
the attaching particles on the surface of the bubble, which in the first approximation
can be equal to the velocity of the particle
- the characteristic velocity of
the attaching particles on the surface of the bubble, which in the first approximation
can be equal to the velocity of the particle ![]() (
(![]() =
=![]() );
); ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() - forces of resistance, gravitation, Archimedes, Basse and joined mass respectively;
- forces of resistance, gravitation, Archimedes, Basse and joined mass respectively;
![]() ,
,![]() ,
,![]() - volume, mass and diameter of
bubble;
- volume, mass and diameter of
bubble; ![]() ,
,![]() ,
,![]() - volume, mass and number of particles, collected by surface of bubble;
- volume, mass and number of particles, collected by surface of bubble;
![]() ,
,![]() - particle mass and diameter; V,
d – flotation complex volume and it’s
characteristic size;
- particle mass and diameter; V,
d – flotation complex volume and it’s
characteristic size; ![]() ,
,![]() ,
,![]() - liquid velocity, density and viscosity;
- liquid velocity, density and viscosity; ![]() - gas density into bubble;
- gas density into bubble; ![]() - gravitational acceleration. Note that the expression
for non-stationary forces in the form of Eq. (3) is strictly justified only for small
Reynolds numbers in the Boussinesq’s approximation. As the characteristic size of flotation
complex can take it effective diameter (from volume)
- gravitational acceleration. Note that the expression
for non-stationary forces in the form of Eq. (3) is strictly justified only for small
Reynolds numbers in the Boussinesq’s approximation. As the characteristic size of flotation
complex can take it effective diameter (from volume) ![]() . The existence of particles on the surface of the bubble further increases
the resistance of the bubble by liquid. In this case, accounting for this
additional forces is done in an approximate form by using in the interaction
force the effective diameter (for example, by volume of flotation complex) instead
of bubble diameter. The resistance coefficient
. The existence of particles on the surface of the bubble further increases
the resistance of the bubble by liquid. In this case, accounting for this
additional forces is done in an approximate form by using in the interaction
force the effective diameter (for example, by volume of flotation complex) instead
of bubble diameter. The resistance coefficient ![]() can be used known expressions from the literature [1-3]. Further, the equation that
determines the position of flotation complex can be written as
can be used known expressions from the literature [1-3]. Further, the equation that
determines the position of flotation complex can be written as
![]() (4)
(4)
For the system of equations (1)-(4) we can assign the following initial conditions ![]() . If the mass of the bubble
is constant
(
. If the mass of the bubble
is constant
(![]() ), equation
(1) is
transformed into the equation for
), equation
(1) is
transformed into the equation for ![]() . Next, let us consider the case of stagnant fluid (
. Next, let us consider the case of stagnant fluid (![]() ) with particles by a constant
sedimentation velocity for which,
) with particles by a constant
sedimentation velocity for which,
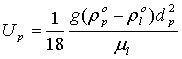 .
.
In this case ![]() .
.
The stationary velocity of bubble. As lifting of bubble it’s speed will strive to stationary value. When the bubble is rising in Stokes
regime (Re<1, ![]() ) for its stationary velocity we have (in case of constant diameter)
) for its stationary velocity we have (in case of constant diameter)
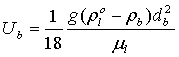
In particular, Stokes regime is realized
for air bubbles with diameter ![]() μm, rising in water.
μm, rising in water.
If the value of Reynolds number of a bubble is not small (Re ≥
1), the Stokes law is not applicable, and hence for the computation of a
stationary velocity ![]() of bubble, we can use the
formula proposed in [4] as
of bubble, we can use the
formula proposed in [4] as
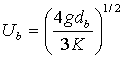 ,
, 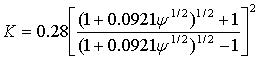 ,
, 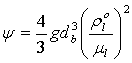
These formulas were used for the numerical analysis presented later.
The change
of bubble diameter. Bubble diameter depends on many factors (pressure and
temperature of fluid and bubbles, Laplace’s pressure at the surface of the
gas-liquid, etc). We suppose that the mass and temperature of the bubble are
constants (![]() ), and
the pressure inside the bubble in any time is balanced by the pressure in the fluid and Laplace’s pressure resulting by the effect of surface
tension. Then for the bubble diameter in stagnant fluid when the pressure in the
fluid is determined only by hydrostatically pressure we have
), and
the pressure inside the bubble in any time is balanced by the pressure in the fluid and Laplace’s pressure resulting by the effect of surface
tension. Then for the bubble diameter in stagnant fluid when the pressure in the
fluid is determined only by hydrostatically pressure we have
![]() ,
,
![]() ,
, ![]()
where õ – coordinate of bubble centre; ![]() - hydrostatically
pressure of liquid, respective to level õ;
- hydrostatically
pressure of liquid, respective to level õ; ![]() - outside pressure; H – height of liquid column;
- outside pressure; H – height of liquid column; ![]() - liquid pressure and
bubble diameter at the initial position õ=0. From here we can get the dependence
of bubble diameter from its coordinates
- liquid pressure and
bubble diameter at the initial position õ=0. From here we can get the dependence
of bubble diameter from its coordinates ![]() , where À is real root of cubic equation
, where À is real root of cubic equation ![]() . Here
. Here
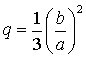 ,
, 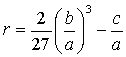 ,
, ![]() ,
, 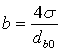 ,
, 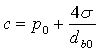
If the bubble is not very small,
so that
the Laplace’s pressure resulting from
the effect of surface tension can be neglected, then the bubble diameter is
defined by formula
![]() . (5)
. (5)
 The influence
of surface mineralization on the intensity of the interaction between bubble and
particles. As the rising bubble surface gradually mineralization occurs, i.e. attached
by particles. Note some features of interaction of particles with bubble in
flotation. When particles attach on bubbles, particles occupy a portion of its
surface, reducing the probability of collisions of other particles with free field
of bubbles surface. Numerous experiments on flotation suggests that particles collide
with the upper hemisphere of rising bubble, and then by liquid flows,
relatively quickly carried away to its bottom hemisphere and slightly affect to
collisions of other particles with a free surface of bubble. Therefore, the
extent of bubbles mineralization, defined by particles concentration in
suspension begins to slow speed of flotation when the particles fills more than
half of the surface bubble [1]. Taking into account these circumstances, here we
propose a scheme approximating taking into account the impact of degree of filling
of bubble’s surface by particles on intensity of capture disperse phase by bubble.
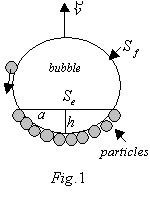
Under these assumptions, filling bubble surface is characterized by height h of spherical segment, and lateral
surface which is covered by particles (Figure 1). If
The influence
of surface mineralization on the intensity of the interaction between bubble and
particles. As the rising bubble surface gradually mineralization occurs, i.e. attached
by particles. Note some features of interaction of particles with bubble in
flotation. When particles attach on bubbles, particles occupy a portion of its
surface, reducing the probability of collisions of other particles with free field
of bubbles surface. Numerous experiments on flotation suggests that particles collide
with the upper hemisphere of rising bubble, and then by liquid flows,
relatively quickly carried away to its bottom hemisphere and slightly affect to
collisions of other particles with a free surface of bubble. Therefore, the
extent of bubbles mineralization, defined by particles concentration in
suspension begins to slow speed of flotation when the particles fills more than
half of the surface bubble [1]. Taking into account these circumstances, here we
propose a scheme approximating taking into account the impact of degree of filling
of bubble’s surface by particles on intensity of capture disperse phase by bubble.
Under these assumptions, filling bubble surface is characterized by height h of spherical segment, and lateral
surface which is covered by particles (Figure 1). If ![]() then the effective area of
collision of particles with bubble is
then the effective area of
collision of particles with bubble is ![]() and if
and if ![]() , then, given the assumption that the particles are fixed only on the
free surface of the bubble, for effective section have
, then, given the assumption that the particles are fixed only on the
free surface of the bubble, for effective section have ![]() . Thus, the expression for the intensity of the collision of particles
with bubble by effects of the bubble surface mineralization can be written as
. Thus, the expression for the intensity of the collision of particles
with bubble by effects of the bubble surface mineralization can be written as
![]() ,
, 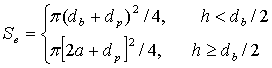 ;
; ![]() (6)
(6)
Here ![]() ,
, ![]() are effectiveness of collisions
of particles with bubble by catching and by gravitational effect [1,2]
are effectiveness of collisions
of particles with bubble by catching and by gravitational effect [1,2]
![]() ,
, 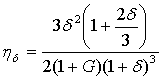 ,
, ![]() ,
, 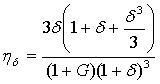 ,
, ![]() (7)
(7)
![]() ,
, ![]() ,
, ![]()
where ![]() is stationary (sedimentary) velocity
of particles in liquid. For transition area 1<Re<80 the laws of motion
of the liquid flow around bubble in analytical form is difficult to get and
therefore, we must use approximate and numerical methods. Using asymptotic
approaches and interpolation of experimental data in [2],
is stationary (sedimentary) velocity
of particles in liquid. For transition area 1<Re<80 the laws of motion
of the liquid flow around bubble in analytical form is difficult to get and
therefore, we must use approximate and numerical methods. Using asymptotic
approaches and interpolation of experimental data in [2], ![]() suggested as
suggested as
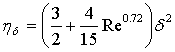 (8)
(8)
Note that the above formulas for intensity of particle collisions with
bubble are just for low values of the Stokes parameter when the particles inertia
forces can be neglected.
To determine the value of h used in Eq. (6), we assume that bubble
surface is covered by monolayer in form of dense packaging. Two specific cases
are studied here: when centers of particles form quadratic (less dense) and triangular
(the most dense) lattice, supposing that the real location are intermediate
between the appointing extreme situations. Volumetric proportion occupied by particles
![]() and the proportion of free area
between particles
and the proportion of free area
between particles ![]() for the extreme situations are
defined as [3]
for the extreme situations are
defined as [3]
![]() ,
, ![]() ,
, ![]() ,
, ![]()
Any periodic
locations of particles centers characterized by parameters ![]() and
and ![]() , and for particles concentrations
, and for particles concentrations ![]() from considerations of
similarity follows
from considerations of
similarity follows ![]() ,
, ![]() . Moreover for quadratic location of particles centers
. Moreover for quadratic location of particles centers ![]() , and for triangular we have
, and for triangular we have ![]() . Then for any intermediate locations of particles taking into account
of closeness of limit values
. Then for any intermediate locations of particles taking into account
of closeness of limit values ![]() and
and ![]() , also
, also ![]() and
and ![]() may be used the approximation
with average coefficient b and average
concentration
may be used the approximation
with average coefficient b and average
concentration ![]() in dense packaging [5]
in dense packaging [5]
![]() ,
, ![]() ,
, ![]() (9)
(9)
Next, we write the
obvious approximate formula ![]() , where
, where ![]() ,
, ![]() are free (from particles)
and complete surface of bubble,
are free (from particles)
and complete surface of bubble, ![]() ,
, ![]() are part of the surface
occupied by the particles and the average free surface between them
respectively. The value
are part of the surface
occupied by the particles and the average free surface between them
respectively. The value ![]() is approximately equal to
sum of middle cross-sections of particles, and for value
is approximately equal to
sum of middle cross-sections of particles, and for value ![]() may be used the
approximation Eq. (9):
may be used the
approximation Eq. (9): ![]() . Then for the height of spherical segment of bubble occupied by
particles we obtain
. Then for the height of spherical segment of bubble occupied by
particles we obtain
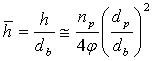 ,
, ![]() ,
, 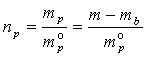 (10)
(10)
Analysis of the results. For example, consider the process
of rising
air bubbles
in the water under normal conditions (Ò=293º
Ê, ![]() =0.1 ÌPà). Values of the defining parameters: height of column
with water H=2 m, diameter of particles
in suspension
=0.1 ÌPà). Values of the defining parameters: height of column
with water H=2 m, diameter of particles
in suspension ![]() 12 μm, real density and mass concentration of particles
12 μm, real density and mass concentration of particles ![]() êg/m3 and
êg/m3 and
![]() êg/m3 (volumetric proportion of disperse phases in suspension
êg/m3 (volumetric proportion of disperse phases in suspension ![]() ). The initial diameter of bubble was changed in range
). The initial diameter of bubble was changed in range ![]() 125 - 1000 μm. As the characteristic values were accepted: stationary
speed of lifting
125 - 1000 μm. As the characteristic values were accepted: stationary
speed of lifting ![]() , height of liquid layer H, time
H/
, height of liquid layer H, time
H/![]() , initial mass of bubble
, initial mass of bubble ![]() . The dimensionless form the system of differential equations (1), (2)
and (4) with closing ratios (3), (5)-(10) was integrated by numerical method.
Evaluation showed that the taking into account of Basse’s force does not significantly
deviate from the calculated velocity obtained without unstable Basse’s forces. In
addition, bubble rather quickly acquires a fixed velocity, so during of such a
short time the bubble can't grab any number of particles. These circumstances
allows to neglect the unstable Basse’s force, and thus the integration of the
system of equations (1)-(4) is considerably simplified.
. The dimensionless form the system of differential equations (1), (2)
and (4) with closing ratios (3), (5)-(10) was integrated by numerical method.
Evaluation showed that the taking into account of Basse’s force does not significantly
deviate from the calculated velocity obtained without unstable Basse’s forces. In
addition, bubble rather quickly acquires a fixed velocity, so during of such a
short time the bubble can't grab any number of particles. These circumstances
allows to neglect the unstable Basse’s force, and thus the integration of the
system of equations (1)-(4) is considerably simplified.
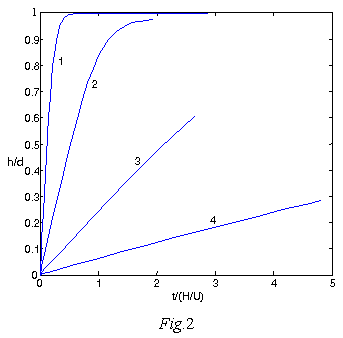 Figure
2 shows the degree of filling of bubble surface by particles depending on the dimensionless
time. Curves 1-4 corresponds to different initial diameter of the bubble
Figure
2 shows the degree of filling of bubble surface by particles depending on the dimensionless
time. Curves 1-4 corresponds to different initial diameter of the bubble ![]() , 250, 500 and 1000 μm. It
can be observed that for the bubbles with diameter less than 250 µm their
surface succeeds to be almost completely clouded by particles before final rising.
For example, for the bubbles with diameter
, 250, 500 and 1000 μm. It
can be observed that for the bubbles with diameter less than 250 µm their
surface succeeds to be almost completely clouded by particles before final rising.
For example, for the bubbles with diameter ![]() μm this happens long before
the final rising, which is not very effective in terms of optimally using the height
of liquid columns. For this it is best is to use the bubbles with a diameter of
about 250 µm, because their surface almost completely mineralized near to the moment
of its final rising.
μm this happens long before
the final rising, which is not very effective in terms of optimally using the height
of liquid columns. For this it is best is to use the bubbles with a diameter of
about 250 µm, because their surface almost completely mineralized near to the moment
of its final rising.
References
- Teorya
i tehnologya flotatsii rud. Pod redaksiiei Î.S. Bogdanova. Ìoskva: Nedra, 1990.
- Yoon R.H., Luttrell G.H. The effect of bubble size on
fine particle flotation. Miner. Process. Extr. Metal. Rev. 1989. No. 5.
p.101.
- Nigmatulin R.I. Osnovy mehaniki geterogennyh
sred. Ìoskva: Nauka,
1978.
- King R.P. Modeling and simulation of
mineral processing systems. Butterworth-Heinemann: London, 2001.
- Goldshtik Ì.À. Prosessy perenosa v zernistom sloye. Novosibirsk:
ITF, 1984.