Технические науки/12. Автоматизированные системы

управления на производстве

К.т.н. Момот В.Е., магистр эл. мех. Сирманов Р.И.

Криворожский технический университет, Украина

Влияние особенностей кинематических связей на динамику электропривода прокатной клети

Улучшение динамических качеств электромеханической системы может быть достигнуто путем учета тесной взаимосвязи процессов в механической и электрической подсистемах. Для упрощения и увеличения жесткости передач конструирование механических кинематических цепей технологических машин имеет тенденцию приближения рабочего органа к электродвигателю. Однако в электромеханической системе прокатной клети обжимного стана выполнить это условие затруднительно, так как реально существующая кинематическая схема главного электропривода, показанная на рис. 1, включает в себя сложную механическую передачу вращающего момента на рабочие валки, которые расположены на расстоянии около 10-и метров от двигателей через промежуточные валы и универсальные шпиндели.

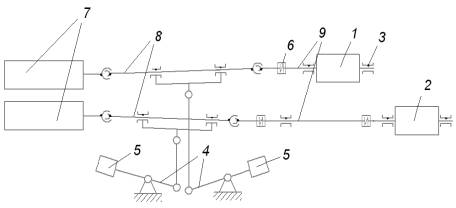
Рис. 1 Кинематическая схема главного электропривода привода прокатной клети

1. электродвигатель верхнего валка; 2. электродвигатель нижнего валка; 3. опорный элемент; 4. рычаги; 5. противовес; 6. муфты; 7. рабочие валки; 8. шпиндели; 9. промежуточный вал.

Известные методы синтеза систем управления электроприводами механизмов с упругими звеньями направлены на снижение динамических нагрузок электрического и механического оборудования различными методами: построением последовательного демпфера; с релейно-модальным управлением; робастным управлением двухмассовых электромеханических систем (ДЭМС). Однако полностью исключить влияние упругих связей, нелинейностей кинематических цепей на динамику привода и обеспечить при этом высокие регулировочные качества системы автоматического регулирования по астатизму затруднительно.

Целью работы является исследование степени взаимодействия электрической и механической части электропривода, влияние на переходные процессы особенностей кинематических связей прокатной клети и повышении качества регулирования введением наблюдающего устройства.

На первом этапе исследований рассмотрено электромеханическое взаимодействие главного электропривода прокатной клети на основании известного подхода, изложенного в [1].

По исходным данным приводного двигателя клети и параметрам второй массы (промежуточный вал, шпиндель и валок) ДЭМС определялись частота свободных колебаний и парциальная частота , по выражениям:

которые составляют соответственно ; коэффициент распределения инерционных масс составляет .

Коэффициент электромеханического взаимодействия определялся по выражению:

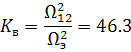
Полученные значения обобщенных показателей дают возможность предварительно судить о динамических свойствах электромеханической системы (ЭМС) в целом и значительном взаимодействии электрической и механической подсистемы.

Влияние особенностей кинематических цепей (упруго деформируемого вала и зазоров в соединительных элементах) на динамику главного привода прокатной клети обжимного стана исследовалась на модели (рис. 2) по расчетным значениям системы регулирования тиристорный преобразователь – генератор – двигатель (ТП-Г-Д) и параметрам двигателя типа П24/160-6.8 и генератора типа П12-40-17к:

Расчетные значения параметров регуляторов первой зоны системы автоматического регулирования (САР) электропривода прокатной клети представлены в таблице 1.

Таблица 1

Тип регулятора	Расчетные параметры
Регулятор напряжения
Регулятор тока
Регулятор скорости

Рис. 2 Модель системы автоматического регулирования координат главного электропривода (I-я зона)

Характер переходных процессов показан на рис. 3, из которых следует время затухания составляет более 2.5 с, амплитуда колебаний по параметрам M₁₂ и ω₁₂ более трехкратных значений от номинальных.

Рис. 3 Момент и скорость второй массы ДЭМС

На втором этапе исследований рассматривалась возможность улучшения динамических свойств главного электропривода прокатной клети так по уменьшению колебаний так и повышению астатизма САР скорости с помощью наблюдателя состояния и введением корректирующих устройств.

Рассматривая поведение ЭМС с упругими связями, трением и зазором, в пространстве состояния в матричном виде [2]:

где X – вектор переменных состояния; A – матрица состояний; - матрица управления; - матрица возмущений и выхода.

Возмущающими воздействиями приняты: упругий элемент, зазор, трение. Для реализации астатической системы принимается вектор состояния наблюдателя в виде:

где - скорость вращения валков; - момент упругости; - скорость вращения двигателя.

Принимая уравнение состояния и выхода наблюдателя в виде:

где - измеряемая переменная скорости вращения двигателя ;

- управляемая переменная наблюдателя (ток якоря ).

Матрицу состояния управления и выхода для двухмассовой системы представим в виде:

В отличии от [3] в систему управления с наблюдателем состояния были введены задатчик интенсивности и фильтр как апериодическое звено.

Моделирование поведения системы производилось при расчетных значениях параметров регуляторов 3-х контурной САР, значениях коэффициентов матрицы модальной обратной связи ( l₁= 1.53·10⁴, l₂=6.46·10⁵ , l₃=10⁶ , l₄=8.03·10³, l₅=370) , при различных видах нагрузки и нелинейных элементов (зазоров).

В результате моделирования получены переходные процессы момента упругости M₁₂(t) и скорости вращения валков ω₁₂(t), приведенные на рис. 4.

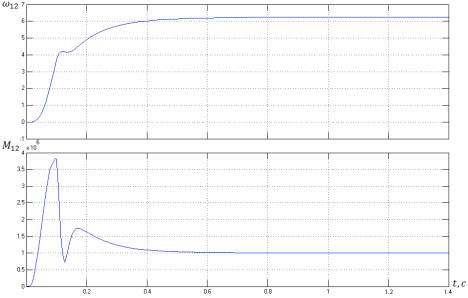
Рис. 4 Переходные процессы момента упругости M₁₂(t) и скорости вращения валков ω₁₂(t)

Таким образом, синтезированная система позволяет получить значительное демпфирование колебаний в течении 0.6-0.8 с, из соответствующим временем восстановления скорости и статической ошибкой по возмущающему воздействию близкой к нулю.

Литература:

1. Задорожний Н.А. Элементы теории электромеханического взаимодействия в двухмассовых системах электропривода с упругими механическими связями. Учебное пособие часть1. - Краматорск 2006. 71 с.

2. Акимов Л.В., Долбня В.Т., Колотило В.И. Системы управления электроприводами постоянного тока с наблюдателями состояния. – Харьков, ХГПУ, 1998. – 117с.

3. Кузнецов Б.И., Осичев А.В. Оптимальное управление главным приводом блюминга в режиме пробуксовки валков. Техническая электродинамика. - Киев, 2000, часть 6. - С. 23-28.