Айтчанов Б.Х.

Республика Казахстан,Казахский национальный технический университет

СИНТЕЗ ЧАСТОТНО-ИМПУЛЬСНЫХ СИСТЕМ УПРАВЛЕНИЯ ТЕХНОЛОГИЧЕСКИМИ ПРОЦЕССАМИ

Системы управления, управляющий алгоритм которых основан на динамической частотно–импульсной модуляции (ДЧИМ), находят широкое применение на практике, в силу высокой степени помехозащищенности и простоты ее технической и программной реализаций.

Повышение требований к качеству современных систем управления требует учета внутренних и внешних случайных возмущений и эффекта запаздывания объекта управления уже на этапе их проектирования и внедрения.

Целью работы является создание методики синтеза динамических частотно-импульсных систем автоматического управления (ДЧИСАУ) технологическими процессами из условий стохастической устойчивости и оптимальности статистического критерия. Основой для этого служат стохастические вольтерровские модели этого класса систем [1] .

Стохастическая динамическая частотно-импульсная система автоматического управления ДЧИСАУ технологическими процессами представляет собой замкнутую систему с отрицательной обратной связью. В прямой цепи системы последовательно включены динамический частотно-импульсный модулятор ДЧИМ и приведенная непрерывная часть (ПНЧ). На входе системы действует случайный стационарный процесс и она функционирует под воздействием белого шума .

Приведенная непрерывная часть описывается функционалом вида [1]

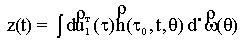, (1)

где (2)

, (3)

, (4)

,

- время запаздывания управляемого объекта, - интенсивность спектральной плотности белого шума .

Задача синтеза динамической частотно-импульсной системы автоматического управления режимными параметрами технологических процессов сводится к выбору управляющего устройства из набора, образованного различными видами динамических частотно - импульсных модуляторов.

Критерием выбора служит функционал следующего вида

, (5) где - функционал, заданный на случайных процессах и .

Как известно [2], модулятор ДЧИМ полностью задаются свойствами функционала фильтра Ф, значением порога импульсного устройства ИУ и формой выходного управляющего импульса .

В [1] получена вольтерровская модель модулятора, применяемого для управления объектами с запаздыванием, в следующем виде

(6) где , (7)

определяются аналогично вектору (2), - характеристика ДЧИМ, учитывающая свойства объектов с запаздыванием.

Выражения (1) и (6) совместно с уравнением замыкания системы служат ограничениями при решении задачи синтеза, характеризующими закономерность протекания процессов в данной системе. Кроме того, как и в других системах, могут быть технические, технологические, экономические и другие ограничения. В общем виде их можно записать как в [3]:

,,

,. (8)

В ограничение (8) входят и условия стохастической устойчивости системы. Например, условие асимптотической устойчивости системы в среднем квадратическом записывается в виде [4]:

, . (9)

Тогда задача синтеза динамической частотно-импульсной системы автоматического управления режимными параметрами непрерывных технологических процессов сводится к нахождению таких функционалов и постоянных параметров , , модулятора, при которых критерий (5) достигает своего экстремального значения и выполняются соответствующие ограничения (1), (6), (8) - (9).

Математическая модель разомкнутой информационно-управляющей системы режимными параметрами с учетом (1), (6) примет вид

, (10)

где , (11)

матрица определяется аналогично (2).

Модели (1), (6), (10) и их взаимные связи позволяют провести процедуру синтеза динамической частотно-импульсной системы автоматического управления режимными параметрами непрерывных технологических процессов, состоящую из следующих этапов.

На первом этапе синтеза строится оптимальная в смысле (5) вольтерровская модель (11). При этом определяются такие элементы матрицы , при которых

,

,, , . (12)

На втором этапе процедуры синтеза проводится реализация найденной оптимальной модели разомкнутой системы вида (10). При заданной модели приведенной непрерывной части ПНЧ (1) задача данного этапа сводится к выбору тех импульсных характеристик математической модели модулятора (6), при которых динамическая частотно-импульсная система автоматического управления непрерывными технологическими процессами, соответствовала бы оптимальной системе (10).

Для этого составим уравнение системы на основе (1) и (6) в следующем виде

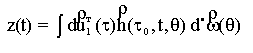, (13)

где

.

Решение уравнений (13) можно получить в виде (10).

Задача третьего этапа заключается в реализации оптимальной вольтерровской модели (6) с помощью эквивалентной ДЧИМ нелинейной системы [2]. На четвертом этапе для выбранного вида ДЧИМ, применяемого для управления объектами с запаздыванием, строятся области настроечных параметров из условия стохастической устойчивости (9).

На пятом этапе проводится параметрическая оптимизация выбранной системы в области параметров, полученной из условия стохастической устойчивости системы. На шестом этапе проводится машинное моделирование системы для оценки качества процесса управления и обоснованности гипотез, использованных в процессе различных аппроксимаций.

В случае неудовлетворительных результатов синтеза, производится коррекция исходных условий решаемой задачи, и процедура синтеза повторяется с нужного этапа.

Разработанная методика синтеза динамической частотно-импульсной системы автоматического управления режимными параметрами непрерывных технологических процессов оформлена в виде диалоговой системы и использована в САПР цифровых систем управления, а также нашла широкое применение при проектировании и внедрении подсистем непосредственного цифрового управления ряда АСУ ТП цветной металлургии, фосфорного и свинцового производств и нефтегазовой отрасли.

Литература:

1. Айтчанов Б.Х. К построению математических моделей одного класса стохастических систем управления объектами с запаздыванием // Энергетика, телекоммуникация и высшее образование в современных условиях. Алматы: АИЭС, 1998. С.108-110.

2. Айтчанов Б.Х. Модели динамических частотно-импульсных систем автоматического управления объектами с запаздыванием // Модели и методы автоматизации управления производственными системами. Алматы: КазНТУ, 1996. Вып. 2. С. 65-73.

3. Попков Ю.С. и др. Идентификация и оптимизация нелинейных стохастических систем. М.: Энергия, 1976. 440 с.

4. Асаубаев К.Ш., Айтчанов Б.Х. Стохастическая устойчивость динамических частотно-импульсных систем управления объектами с запаздыванием // Вестник КазНТУ. Алматы: КазНТУ, 1997. С.49-53.