Броншпак Г.К.; д.э.н., Бубенко П.Т.; к.т.н. Чернышов С.И.

Харьковская национальная академия городского хозяйства

Концерн «АВЭК»

Страховая компания «ЛЕММА»

Анализ статистических методов с точки зрения их эффективности для проведения бенчмаркинговых исследований

Методология бенчмаркинга предполагает сравнение деятельности своей организации с конкурентом и ликвидацию отставания. Очевидно, целесообразной явилась бы количественная оценка такого отставания. Для ее получения могут быть использованы статистические методы определения расстояний в пространствах набора признаков. Однако имеется целый арсенал подобного рода методов и соответственно представляет интерес выбрать из них наиболее эффективный применительно к рассматриваемой постановке задачи. В качестве основного источника исходной информации принят раздел 5 работы [1].

Факторный анализ предполагает, что внутренние связи между признаками можно выразить посредством сравнительно небольшого количества линейных корреляций. Согласно методу главных факторов, специальным образом выстраивается матрица корреляций, которая должна удовлетворять условию минимальности ранга. Вместе с тем соответствующая процедура численной реализации является достаточно сложной и в ряде случаев не дает гарантий достоверности получаемого результата.

Компонентный анализ позволяет свести задачу к определению общих факторов с помощью некоторым образом взвешенных сумм исходных признаков. Для снижения трудоемкости производимых при этом вычислений разработан центроидный метод. С его помощью задача сводится к минимизации некоторой квадратичной формы.

Метод -коэффициентов. В данном случае осуществляется предварительная группировка признаков по их сравнительной связности между собой. С помощью -коэффициентов устанавливается завершение формирования группы по показателю порогового значения.

В целом для достижения преследуемой цели потенциал методов факторного анализа является избыточными. В тоже время их реализация может быть достаточно затруднительной. Следует отметить, что методы факторного анализа предназначены для большого количества признаков. Если же их не более 10, то достаточными оказываются средства корреляционного анализа [2].

Метод многомерных группировок. Используется анализ принадлежности признаков к группам однородных показателей качественного уровня в разрезе некоторого количества наблюдений. С помощью статистических оценок выстраивается матрица отношения значений каждого признака и средней арифметической. Затем привлекаются методы регрессионного анализа.

Эта методика является сравнительно несложной и широко применяется на практике. Для бенчмаркинговыъх процедур она представляет интерес в случаях, когда информация о признаках является неоднозначной. То есть, данный метод может быть вспомогательным для базисного алгоритма. Он должен в большей мере учитывать особенности бенчмаркинга.

Метод многомерного динамического ряда. На основании качественного анализа признаков находится последовательность чисел, характеризующих изменение во времени укрупненного фактора. Данный подход органично сочетается с многомерными группировками и регрессионным анализом, позволяя идентифицировать зависимости и строить прогнозные оценки. Так как бенчмаркинг в деятельности фирмы – непрерывный процесс – эти возможности представляют очевидный интерес. Например, для выяснения стратегии, которой придерживается конкурент. Тем не менее, в качестве базиса он, как и предыдущий метод, не подходит.

Метод индексов. Статистический индекс – это показатель относительного изменения уровня некоторого явления с эталоном, который принят для сравнения. Такого рода идея весьма созвучна методологии бенчмаркинга и будет развита ниже.

Метод экстремальной группировки параметров (ЭГП) в задачах статики. Подразумевается сопряжение методов главных компонент и центроидного. Максимизация используемых функционалов производится по разбивке признаков на группы и по выбору факторов. Процедура является итерационной. Используется чередование функционалов, обеспечивающих непрерывность весовых коэффициентов и быструю сходимость. Метод ЭГП широко применяется для построения обобщенных индикаторов (ОИ).

Динамический метод ЭГП. Построение ОИ осуществляется в виде линейной комбинации динамической и статической составляющих. Первая отражает тренд среднего уровня, вторая – колебание относительно него значений соответствующего показателя, характеризуя индивидуальные особенности процесса

Методы кластерного анализа позволяют разделять некоторое множество, которому принадлежат рассматриваемые объекты, на непересекающиеся подмножества (кластеры) по формализованному критерию сходства. В сравнении с факторным анализом, реализация алгоритмов данного метода является гораздо менее трудоемкой. Вместе с тем, постановки задач, для которых предназначен кластерный анализ, также более обширны, чем того требует бенчмаркинг.

Комбинированный метод, сочетающий принципы кластерного анализа и статистических индексов. Данный метод, называемый также таксономическим, идеально приспособлен для проведения бенчмаркинговых исследований. «Методы таксономии особенно эффективно применяют для сопоставления различных подсистем (предприятий) между собой по уровню технического развития, построенного на обобщенных индикаторах» [1, с. 155].

Пусть имеется объектов, каждый из которых характеризуется количественными признаками. Объекты оцениваются на соответствие своих признаков выбранному эталону. Ему присваиваются наивысшие значения по всем признакам рассматриваемой выборки.. Данные представляются в виде матрицы , где – значение -го признака -го объекта.

Расстояния между объектами и эталоном находятся следующим образом:

,
где , – стандартизированные координаты соответственно эталона и объектов.

Среднее расстояние и среднее квадратичное отклонение по всей совокупности объектов находятся по формуле:

.

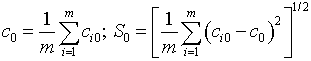Обозначим , где – число, зависящее от закона распределения. В таком случае таксономический показатель объекта . Чем ближе его значение к единице, тем более совершенным является -й объект. Охарактеризованный метод без принципиальных осложнений распространяется также и на задачи проведения сравнений в динамической постановке [1, с. 157-162].

Упомянутая выше стандартизация предполагает приведение признаков к безразмерному виду, что не вызывает затруднений. Значительно более принципиальным является отличие между признаками по значимости, которое наблюдается практически в любой ситуации. Без учета данного обстоятельства результаты бенчмаркингового исследования могут оказаться ошибочными.

В связи с этим для определения расстояния между объектами должно использоваться выражение:

,
то есть, взвешенное евклидово расстояние, где – коэффициенты сравнительной значимости признаков.

Определение коэффициентов в общем случае может производиться путем экспертного оценивания. Как представляется, для этого наиболее эффективен метод анализа иерархий (МАИ) [3]. Этот метод можно назвать «человеко-машинным», так как он оптимально сочетает возможности каждой из указанных сторон. Человеку присуща способность аналитического мышления, тогда как компьютер легко оперирует с большим числом формализованных признаков.

МАИ состоит в декомпозиции проблемы на максимально простые компоненты и обработке экспертных суждений путем парных сравнений. В результате выстраивается иерархия взаимодействия элементов и суждения характеризуются численно. МАИ использует процедуры: синтез множественных суждений; получение приоритетных критериев; нахождение альтернативных решений. Для реализации (на субъективной основе) парных сравнений разработана шкала относительной важности, которая убедительно продемонстрировала свою практическую значимость.

Применительно к рассматриваемому случаю, в первую очередь, нужно выяснить мнение экспертов о том, какой из нескольких вариантов выбора значений наиболее приемлем. Вначале экспертам требуется определить критерии оценки этих вариантов, которые явились бы наиболее представительными. В частности, объем экспорта, доля рынка, финансовая результативность и т. п. Путем парного сравнения этих критериев в привязке к упомянутой шкале формируется соответствующая матрица. Ее обработка с помощью программных средств позволяет получить вектор приоритета критериев.

Затем в разрезе той же шкалы варианты принятия решений сравниваются попарно для каждого критерия, что позволяет построить матрицы аналогичного вида. Их таким же образом обрабатывает компьютер для получения соответствующих векторов. В результате умножения последних на вектор приоритетов выстраивается рейтинг вариантов выбора коэффициентов .

Литература

1. Кучин Б.Л., Седых А.Д., Овчаров Л.А. Научно-техническое прогнозирование развития систем газоснабжения. – М.: Недра, 1987. – 256 с.

2. Дружинин Н.К. Математическая статистика в экономике. – М.: Статистика, 1971. – 264 с.

3. Саати Т., Кернс К. Аналитическое планирование. Организация систем. – М.: Радио и связь, 1991. – 224 с.