Математическое моделирование задач ТММ

Лебедева Г.И., Лебедев Е.П., Кудин В.В.

Белорусский национальный технический университет

Математическое моделирование в настоящее время является неотъемлемой частью любого научного исследования. С помощью моделей появляется возможность более глубокого исследования объекта и выбора с минимальными затратами оптимального решения. Средства и методы построения модели могут быть различными. Это зависит от наличия соответствующей информации об объекте исследования, квалификации исследователя и т.д.

В настоящей работе математическое моделирование осуществлялось для различных движений толкателя. Исследования основывались на использовании рядов Фурье и корреляционно – регрессионного анализа.

Так как механизмы ТММ (например, кулачок) совершают сложные колебания их в большинстве случаев лучше описать функцией, представляющей собой сумму ряда простых гармонических колебаний (рядом Фурье):

,.

где k – номер гармоники,

, .

Нами были построены модели для ряда движений толкателя для ускорения, скорости и пути перемещения. Расчеты производились по специально разработанной программе.

Полученные в результате расчетов коэффициенты рядов Фурье приведены в таблице 1.

Таблица 1

Гармоники	S (путь)		(скорость)		(ускорение)
	ak	bk	ak	bk	ak	bk
1	-0,0154	0,002	-0,0048	0,0386	0,104	0,0135
2	0,0009	0,0008			-0,00165	-0,0257
3	0,0006	-0,0003			-0,0258	-0,0005
4	-0,00012	-0,00027			-0,0157	0,01929
6	-0,0016	0,00006			-0,004	0,0022
8	0,00002	-0,00016
11	-0,00017	0,00006
12	0,000078	0,00002
А0	0		-0,00012		0

Описание ускорения осуществлялось по единой кривой.

Построенные модели довольно близки к фактическим данным и хорошо их описывают.

Учитывая сложность графика ускорения, мы его описали ещё и комбинированным методом с использованием корреляционно–регрессионного анализа (для первой половины графика ) и ряда Фурье (для второй половины ). В результате были получены следующие модели ускорения толкателя:

, где ; , , R=0.9

Соответствующее описание скорости рядом Фурье по выделенным участкам имеет числовые значения коэффициентов, приведенных в таблице 2.

Таблица 2

Гармоники	(скорость)		(скорость)
	ak	bk	ak	bk
1	-0,0172	-0,0043	0,025	0,0061
2	-0,0034	-0,002	-0,0013	-0,00061
3	-0,0011	-0,0011
4	-0,00035	-0,00045	-0,00045	-0,00065
5	-0,0001	-0,00036
6	-0,00018	-0,00002
	А0=0,0224		А0=-0,0227

Расчетные значения скорости очень близки к экспериментальным.

Известно, что с помощью дифференцирования осуществляется переход от пути к скорости и ускорению. Нами было выполнено исследовании по обратному переходу, т.е. от модели ускорения к скорости и от скорости к пути перемещения толкателя. Установлено, что такие перемещения можно выполнить с помощью формул:

, где (1)

, где (2)

Расчетные значения и по формулам (1) и (2) получаются близкими к экспериментальным. Графики этих функций, рассчитанных по формулам (1), (2) и по ряду Фурье совпадают по форме и очень близки друг к другу (рисунки 1 и 2). Для случая отдельного описания ускорения по выделенным участкам совпадение идеальное (рисунок 3).

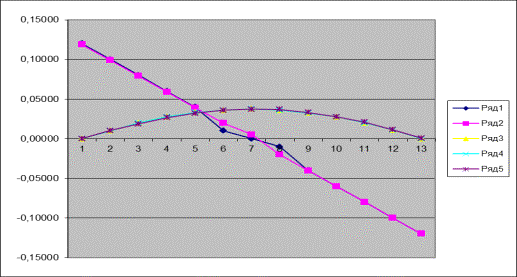
Рисунок 1

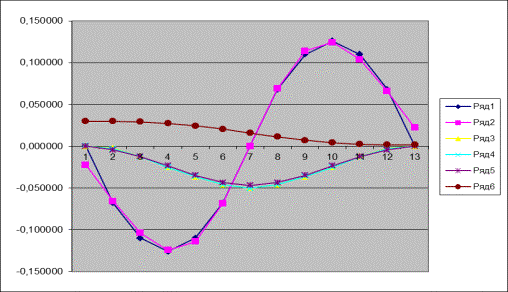
Рисунок 2

При общем описании ускорения единой кривой наблюдается небольшое отклонение у пути в последних двух точках (рисунок 3).

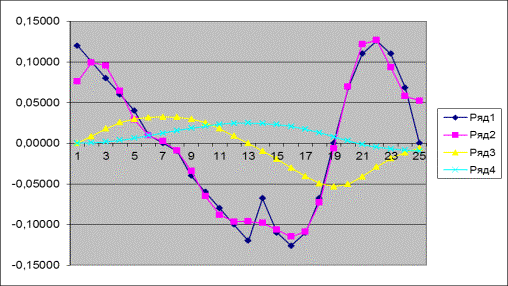
Рисунок 3

Таким образом, можно сказать, что формулы (1) и (2) работают и что полученные модели могут быть рекомендованы для практического использования. Их применение существенно сократит трудоемкость инженерных расчетов и повысит качество разработок.

Литература

1. Вентцель Е.С. Исследование операций. М.:Сов. радио, 1972,-400с.

2. Монахов В.М. Методы оптимезации. М.:Просвещение, 1978,-342с.