Дзюбич И.С., студент

Радченко С.Г., д.т.н., професор

НТУУ «КПИ», г. Киев, Украина

 

Нерешонные проблемы статистического моделирования процессов резания

При получении многофакторных статистических моделей необходимо решить следующие основные проблемы.

1.Выбрать план эксперимента, который обеспечил бы наилучшие воз­можные критерии качества получаемых моделей.

2.Предложить методологию формализованного выбора структур моде­лей, которые до проведения эксперимента исследователю не известны[1].

3.Устойчиво оценить коэффициенты моделей.

Сложные системы, объекты, процессы обычно характеризуются не­сколькими критериями качества уw. Структуры статистических моделей, в общем случае, будут для разных уw различными, что необходимо учитывать при выборе плана эксперимента и структур моделей. Конкретный вид струк­тур моделей обычно исследователю заранее не известен[2].

В статистические модели необходимо вводить управляемые факторы Хі эффекты, которые влияют на критерии качества статистически значимо. С увеличением числа факторов структура модели усложняется, что приводит к увеличению числа опытов N в плане эксперимента. Для установления значи­мо влияющих факторов можно провести отсеивающий эксперимент по мето­ду случайного баланса [3,c.72-81] или по его модификации методу ветвя­щейся стратегии. Это потребует дополнительные ресурсы и время для прове­дения исследования. Поэтому можно рекомендовать первоначально провести оптимизацию факторов, и в модель вводить только те факторы, которые бу­дут изменяться в процессе функционирования системы, а некоторые из фак­торов будут иметь оптимальные постоянные значения. Метод оптимизации - случайный поиск с использованием ЛПτ равномерно распределенных после­довательностей позволяет оптимизировать десятки факторов при сравни­тельно малом числе опытов - порядка 32.

Число различных уровней si, для факторов Xi, необходимо выбирать та­ким, чтобы адекватно описать влияние фактора на критерии качества уw. Число уровней должно быть на единицу больше максимально необходимой степени полинома фактора Xi для адекватного описания его влияния в стати­стической модели. С увеличением числа уровней si, факторов сложность опи­сания системы и число необходимых опытов увеличивается, что приводит к увеличению затрат ресурсов. Для качественных факторов и факторов с дис­кретными уровнями их число задается перечислением их уровней.

При использовании ЛПτ равномерно распределенных последовательно­стей в качестве планов экспериментов число уровней для непрерывных фак­торов равно числу опытов в плане эксперимента, т. е. si = N, что достаточно для адекватного описания. В случае необходимости при использовании ЛПτ равномерно распределенных последовательностей число уровней для непре­рывных факторов может быть понижено до необходимых значений.

Выбор числа уровней для непрерывных факторов должен проводиться на основании логически-профессионального анализа предметной области ис­следования.

Число опытов N в плане эксперимента зависит от числа факторов Xi и числа уровней  si факторов. Все планы экспериментов по числу опытов под­разделяются на полные и дробные факторные эксперименты.

Для многофакторных регулярных планов экспериментов принята сле­дующая форма записи для обозначения плана эксперимента:

где s1,s2,…,sk - число различных уровней для числа факторов к1 ,к2, ..., кк.

 

Полный факторный эксперимент - эксперимент, включающий все воз­можные комбинации уровней изучаемых факторов при выбранном числе уровней по каждому фактору. Число опытов Nп =

Получаемые при проведении эксперимента значения откликов ywul (w - текущее значение критерия качества, 1 ≤ w ≤ т, и - текущее значение номера опыта, 1 ≤ u ≤ N; l- текущее значение номера повторного опыта, 1≤l≤п) есть результат суммарного влияния управляемых, неуправляемых и некон­тролируемых факторов. Влияние управляемых факторов Х(.) оценивается в виде получаемой статистической модели . Влияние неуправляемых Z(.) и неконтролируемых У(.) факторов оценивается в виде дисперсии воспроизво­димости опытов s2восп. Если влияние этих факторов значитель­ное и дисперсия s2восп относительно велика, то многие коэффициенты модели   могут оказаться статистически незначимыми. Одним из новых подходов для повышения воспроизводимости результатов повторных опытов экспери­мента в неоднородных условиях (уменьшения значений s2восп) является ис­пользование поправки RASТА (подразд.4.5.).

При увеличении числа факторов  число опытов Nп полного факторного эксперимента быстро растет, и их выполнение становится практически невоз­можным. Необходимо использовать дробный факторный эксперимент с чис­лом опытов Nд < Nп, который представляется определенной частью полного факторного эксперимента. Число уровней по каждому фактору такое же, как и в полном факторном эксперименте.

Для дробных факторных экспериментов можно рекомендовать выби­рать число опытов с учетом эмпирической формулы

,

 

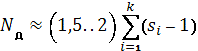где  si - число уровней i-го фактора; 1 ≤ i ≤ к:   

       k - общее число факторов

Меньше рекомендуемого число опытов использовать не следует, так как коррелированность взаимодействий факторов будет сравнительно высо­кой, что не позволит получить устойчивое оценивание коэффициентов моде­ли.

Выбор начальных условий аппроксимации эмпирической зависимости во многом определяет качество статистических моделей и требует использо­вания информации, как в математической части, так и в предметной области исследования.

Литература:

1.     Моделирование и анализ устойчивости многофакторных регрессионных моделей / Радченко С.Г. – К.: ТОВ «Задруга»,2008. – 108с.

2.     Особенности использования статистической методологии в моделировании сложных систем и процессов / Радченко С.Г. – Вісник Харк. нац. техн.ун-ту сільськ. гос-ва. ім. Петра Василенка. - 2008.- Вип.68.- 249-252с. 

3.     Оптимизация технологических процессов в машиностроении / В.В.Душинский, Е.С.Пуховский,С.Г.Радченко; под. общ.ред. Г.Э.Таурита. – К.:Техніка, 1977. -176с.