Математика / 5. Математическое моделирование

К. пед. н. Бондар М. В., Махлай А.

Вінницький торговельно-економічний інститут Київського національного торговельно-економічного університету, Україна

Виробничі функції в економіко-математичному моделюванні

У реальному житті в межах конкретних технологій підприємець прагне знайти найкраще поєднання чинників виробництва, з тим щоб досягти найбільшого виходу продукції. Кожна фірма має свою виробничу функцію, яка характеризує технологічний спосіб виробництва, вибраний фірмою. Функція виробництва описує те, що можливо здійснити технічно за умови, що фірма діє ефективно.

Економічно ефективним вважається спосіб виробництва, який мінімізує альтернативну вартість всіх видів витрат виробництва заданого обсягу продукції.

Економічна ефективність залежить від ринкової ціни різних видів ресурсів.

Існує багато технологічно ефективних способів виробництва і лише один економічно ефективний – той, який на даний момент забезпечує мінімальні грошові витрати фірми за даного рівня цін на використовувані вхідні ресурси.

Виробнича функція – це економетрична модель, яка кількісно описує зв’язок основних результативних показників виробничо-господарської діяльності з факторами, що визначають ці показники. До основних показників можна віднести дохід, прибуток, рентабельність, продуктивність праці, собівартість.

Перше поняття виробничої функції пов’язане з математичним моделюванням технологічної залежності між обсягом продукції, що випускається, і кількісними характеристиками витрат ресурсів. Звідси і назва функції «виробнича». Уперше така функція була побудована американськими дослідниками Коббом і Дугласом ще в 30-ті роки ХХ ст. за даними про функціонування обробної промисловості США протягом двадцяти років і є класичним прикладом економетричного моделювання [2].

Функція Кобба-Дугласа (CDPF) належить до найвідоміших виробничих функцій, що набули широкого застосування в економічних дослідженнях, особливо на макрорівні.

Класична виробнича функція Кобба-Дугласа має вигляд:

,

де Q – обчислений або очікуваний індекс виробництва продукції обробної промисловості за деякий характерний інтервал часу;

L – індекс зайнятості в обробній промисловості;

K – індекс постійного капіталу;

A – позитивне постійне число, що характеризує технологію виробництва.

Функція Кобба-Дугласа має такі властивості:

1) коефіцієнт α показує, на скільки відсотків зміниться обсяг випуску продукції, якщо витрати праці зміняться на 1%, а витрати капіталу залишаться незмінними. Такий показник називається коефіцієнтом еластичності випуску за витратами праці;

2) коефіцієнт β є коефіцієнтом еластичності випуску за витратами капіталу;

3) сума параметрів α+β описує масштаб виробництва.

Якщо ця сума дорівнює одиниці, маємо постійний масштаб виробництва. А це означає, що зі збільшенням обох виробничих ресурсів на одиницю обсяг продукції також зросте на одиницю.

Якщо сума менша одиниці, то масштаб виробництва спадний, тобто темпи зростання обсягу продукції нижчі за темпи зростання обсягу ресурсів.

Якщо сума перевищує одиницю, маємо зростаючий масштаб: темпи зростання обсягу продукції перевищують темпи зростання обсягу виробничих ресурсів [1].

Отже, економетрична модель виробничої функції дає змогу проаналізувати виробничу діяльність, щоб визначити шляхи підвищення її ефективності.

Обґрунтованість такого аналізу цілковито залежить від достовірності моделі та її адекватності відповідному реальному процесу.

Окрім вище вказаної функції для аналізу виробничої діяльності фірм використовуються наступні:

1. Функція з фіксованими пропорціями чинників (функція Леонтьєва):

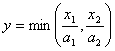, де а₁, а₂ – параметри моделі.

Функція Леонтьєва призначена в основному для моделювання строго детермінованих технологій, які не допускають відхилення від технологічних норм і нормативів щодо використання ресурсів на одиницю продукції. Як правило, вона використовується для формалізованого опису дрібномасштабних або цілком автоматизованих об’єктів.

2. Лінійна функція:

.

Лінійна функція застосовується для моделювання великомасштабних систем (велика галузь, народне господарство в цілому), у яких випуск продукції є результатом одночасного функціонування великої кількості різноманітних технологій. Особливу роль відіграє гіпотеза постійності граничних виробничих чинників чи їх необмеженого заміщення.

3. Функція Аллена:

.

Функція Аллена призначається для формалізованого опису виробничих процесів, у яких надмірне зростання будь-якого з чинників негативно впливає на обсяг випуску продукції. Зазвичай така функція використовується для формалізованого опису дрібномасштабних виробничих систем з обмеженими можливостями переробки ресурсів.

4. Функція постійної еластичності заміщення чинників (функція CES):

.

Функція CES застосовується у разі відсутності точної інформації щодо рівня взаємозаміни виробничих чинників, і разом з тим є підстави вважати, що цей рівень суттєво не зміниться за зміни обсягів залучених ресурсів, тобто коли економічна технологія має властивість певної стійкості щодо певних пропорцій чинників. Функція CES (за наявності засобів оцінки її параметрів) може використовуватись для моделювання систем будь-якого рівня.

5. Функція Солоу:

.

Характеризується тим, що величина відсоткової зміни граничної норми заміщення чинників, що пов’язане зі зміною одного з чинників на один відсоток, не залежить від початкового рівня чинників. Функція Солоу може використовуватись у моделюванні системи різних масштабів.

6. Багаторежимна функція:

.

Багаторежимна функція – одна з найзагальніших. Вона використовується для формалізованого опису та моделювання процесів, у яких рівень віддачі кожної додаткової одиниці ресурсу стрибкоподібно змінюється залежно від співвідношення чинників. Функцію доцільно застосовувати за наявності апріорної інформації щодо кількості режимів k, а інколи й щодо величини «перехідної» області між режимами (чим більше , тим чіткіше виокремлюються режими).

7. Багатофакторні виробничі функції.

В економіко-математичному моделюванні широко використовують багатофакторні виробничі функції.

Один із найбільш раціональних способів переходу від двофакторних до багатофакторних функцій полягає в наступному: двофакторна функція . Аргумент x₂ цієї функції розглянемо як узагальнений показник, що залежить також від двох інших факторів x₃, x₄: , де ₂ – деяка функція. Підставляючи цей вираз у формулу, отримаємо трифакторну функцію: , що виражає залежність показника від аргументів x₁, x₃, x₄ [3].

Цей процес можна продовжити, вважаючи, зокрема, що х₃, у свою чергу, залежить від деяких чинників. У загальному вигляді: якщо задано (п–1) двофакторних функцій: ,,…,, то дістанемо n-факторну функцію: y=f(,…,), у результаті послідовної підстановки їх. Операція такої підстановки (суперпозиції) має очевидний економічний сенс: другий аргумент, наприклад двофакторної функції, послідовно подається у вигляді залежності від показників нижчих (деталізованих) рівнів.

Виробнича функція свідчить, що існує багато варіантів виробництва певного обсягу продукції за рахунок певного набору факторів виробництва.

Поліпшення технологічних параметрів, що максимально збільшують обсяг виробництва певного виду продукції, завжди відображається у новій виробничій функції.

Література:

1. Гончарова Н.М. Мікроекономіка: навч. посібник для студ. вищих навч. закл. / Н.М. Гончарова; Міжрегіональна академія управління персоналом. – К. : МАУП, 2005. – 304 с.

2. Задоя А.О. Мікроекономіка: Курс лекцій та вправи: навч. посібн. / А.О. Задоя. – 2-ге вид., стер. – К. : Т-во "Знання", КОО, 2002. – 211 с.

3. Лісовицький В.М. Мікроекономіка: навч. посібн. / В.М. Лісовицький. – 3-є вид., доп. і доробл. – К. : Кондор, 2007. – 164 с.