Measurement Error

Smailova A.D., Iksan Zh.M., Raiymzhanova A.N.

Pavlodar Station University named after S. Toraigyrov,

Republic of Kazakhstan

The true score theory is a good simple model for measurement, but it may not always be an accurate reflection of reality. In particular, it assumes that any observation is composed of the true value plus some random error value. But is that reasonable? What if all error is not random? Isn't it possible that some errors are systematic, that they hold across most or all of the members of a group? One way to deal with this notion is to revise the simple true score model by dividing the error component into two subcomponents, random error and systematic error. here, we'll look at the differences between these two types of errors and try to diagnose their effects on our research.

Figure 1.

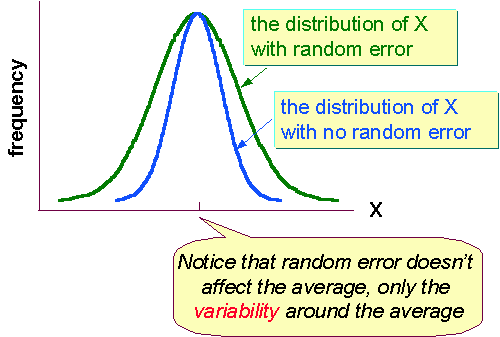
Random error is caused by any factors that randomly affect measurement of the variable across the sample. For instance, each person's mood can inflate or deflate their performance on any occasion. In a particular testing, some children may be feeling in a good mood and others may be depressed. If mood affects their performance on the measure, it may artificially inflate the observed scores for some children and artificially deflate them for others. The important thing about random error is that it does not have any consistent effects across the entire sample. Instead, it pushes observed scores up or down randomly. This means that if we could see all of the random errors in a distribution they would have to sum to 0 -- there would be as many negative errors as positive ones. The important property of random error is that it adds variability to the data but does not affect average performance for the group. Because of this, random error is sometimes considered noise.

Figure 2.

Systematic error is caused by any factors that systematically affect measurement of the variable across the sample. For instance, if there is loud traffic going by just outside of a classroom where students are taking a test, this noise is liable to affect all of the children's scores -- in this case, systematically lowering them. Unlike random error, systematic errors tend to be consistently either positive or negative -- because of this, systematic error is sometimes considered to be bias in measurement.

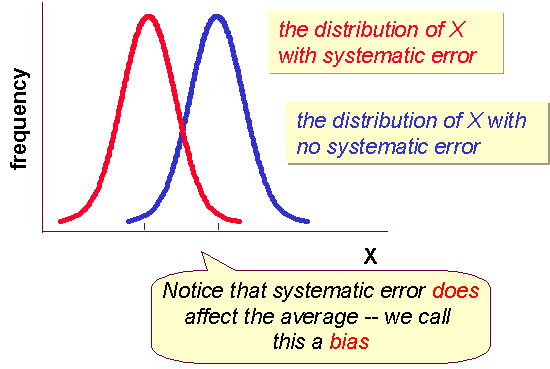
Figure 3.

Reducing Measurement Error. So, how can we reduce measurement errors, random or systematic? One thing you can do is to pilot test your instruments, getting feedback from your respondents regarding how easy or hard the measure was and information about how the testing environment affected their performance. Second, if you are gathering measures using people to collect the data (as interviewers or observers) you should make sure you train them thoroughly so that they aren't inadvertently introducing error. Third, when you collect the data for your study you should double-check the data thoroughly. All data entry for computer analysis should be "double-punched" and verified. This means that you enter the data twice, the second time having your data entry machine check that you are typing the exact same data you did the first time. Fourth, you can use statistical procedures to adjust for measurement error. These range from rather simple formulas you can apply directly to your data to very complex modeling procedures for modeling the error and its effects. Finally, one of the best things you can do to deal with measurement errors, especially systematic errors, is to use multiple measures of the same construct. Especially if the different measures don't share the same systematic errors, you will be able to triangulate across the multiple measures and get a more accurate sense of what's going on.

References

1. Кazovsky L.G. Particle analysis using forward scattering data. // Applied Optics. - 1984. - V.23 (3). - P.448-454 (In russian).

2. Fetisov V.S., Kharisova Z.I., Intelligent liquid analyzer for measurements of turbidity and suspended particles concentration // Ecological systems and devices - 2014 - №5. - P.3-9 (In russian).

3. www.socialresearchmethods.