Зайцева Т.А., Осачий М.В., Кузенков А.А.

Днепропетровский национальный университет им. О.Гончара, Украина

ПРИМЕНЕНИЕ МатематическоГО моделированиЯ ДЛЯ ОЦЕНКИ динамики МЕЖЛИЧНОСТНЫХ ОТНОШЕНИЙ СРЕДИ молодежи

Развитие методов междисциплинарных исследований позволяет по-новому взглянуть на некоторые научные проблемы. Развитие синергетики и нелинейной динамики дает новое видение единства мира. По сути, существует очень небольшое число различных сценариев самоорганизации и переходов порядок – хаос в нелинейных открытых диссипативных системах, которые возникают практически везде при моделировании явлений, связанных с социумом. Очень важно правильно ставить проблему, корректно формулировать вопросы, на которые требуется получить ответ, и оценивать те рамки, в которых полученный ответ имеет смысл. Для математического моделирования в психологии достаточно широко используется дифференциальные модели. Кафедрой общей психологии и педагогики и кафедрой компьютерных технологий ДНУ им. О. Гончара проводилось исследование уровня эмпатии среди молодежи в возрасте 17-22 лет. Первичная обработка данных осуществлялась при помощи пакета SPSS. Построена модель уровня эмпатии среди молодежи, в которой модель Лотки-Вольтерры использована в качестве базовой. В общем виде, система представлена следующим образом:

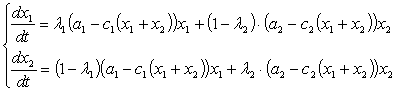(1)

где - численность группы с индексом .

- часть членов группы с индексом , которые могут изменить их на качества группы с индексом (будем называть такие параметры коэффициентами перехода) .

- коэффициент потенциального роста -й группы.

- уровень межгрупповой конкуренции группы с индексом и другими группами.

- размерность задачи.

- “емкость” системы для -ой группы.

Система имеет три особые точки , , и условную стационарную прямую общего вида которая возникает при условии .

Было проведено исследование изменение топологии фазовых траекторий модели при изменении ее параметров. На рис.1(а) представлено фазовый портрет системы (1)

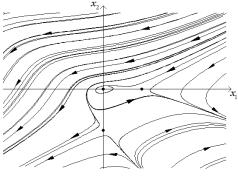
Рис.1. Фазовый портрет системы (1) при , , , ,, ,

Рис.2. Динамика фазовой траектории при изменении параметра на промежутке с шагом

Изменяя значения параметра на промежутке с шагом получим график изменения фазовой траектории относящейся к начальным координатам . Соответствующий график представлен на рис.2. При , , , , , , в системе возникает дополнительная стационарная прямая (рис.3).

Рис.3. Фазовый портрет системы (1) при , , ,

, , ,

На рис.4 (а-б) представлена динамика фазовых траекторий взятых ниже и выше атрактора.

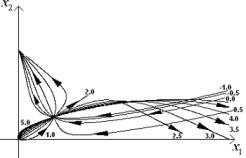
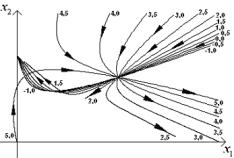
Рис.4. Динамика фазовой траектории “а” - , “б” - рис.3. при изменении параметра на промежутке с шагом .

Полученные результаты свидетельствуют о высокой степени нелинейности разработанной модели. При этом незначительное изменение параметров системы может привести к существенным изменениям топологии фазового пространства модели. Как показали исследования результаты математического моделирования тесно пересекаеться с результатами получеными путем психологического исследования о котором говорилось выше.