Вейвлет-преобразования в биометрической идентификации по подписи

За последние несколько лет получили достаточно широкое распространение различные методы обработки данных на основе вейвлет-преобразований. Вейвлеты широко применяются для фильтрации и предварительной обработки данных, анализа состояния и прогнозирования ситуации на фондовых рынках, распознавания образов, при обработке и синтезе различных сигналов, например речевых, медицинских, для решения задач сжатия и обработки изображений, при обучении нейросетей.

Особенно актуальна принципиальная возможность вейвлетов представлять нестационарные сигналы, например, состоящие из разных компонент, действующих в разные промежутки времени, модулированные сигналы. Такие сигналы в наше время находят более широкое применение, чем стационарные или квазистационарные (искусственно сводящиеся к стационарным) сигналы. Также они включены в расширения новейших систем компьютерной математики (СКМ), таких как MATLAB , Mathcad и Mathematica .

В последнее время увеличивается интерес к биометрическим системам доступа, которые широко применяют вейвлет-анализ.

Актуальна тема точной идентификации личности. Лучше всего этого можно добиться, снимая биометрические показатели с человека, так как они уникальны для каждого индивидуума и не могут быть утеряны.

Порядок работы систем динамической аутентификации:

1. преобразование неэлектрических величин (координат конца пера, звукового давления) в электрические сигналы;

2. оцифровка входных электрических сигналов;

3. масштабирование амплитуд входных сигналов, приводящее их к некоторому эталонному значению;

4. приведение сигналов к единому масштабу времени;

5. вычисление вектора (матрицы) контролируемых биометрических параметров;

6. режим работы системы (обучение или аутентификация) определяет совокупность операций, осуществляемых с уже сформированным вектором параметров.

Идентификация по динамике подписи, вводимой в компьютер, осуществляется на основе данных о колебаниях пера, при воспроизведении подписи в трёхмерном пространстве (X, Y - координаты и Z - давление на планшет).

Системы, использующие одну из функций времени X(t), Y(t) или Z(t) обеспечивают вероятность ошибки 0,1. Если использовать две функции, то вероятность ошибки 0,01. Для трёх функций вероятность ошибки 0,003. Система идентификации по почерку предполагает наличие планшета, например, Wacom, CalCom, Genius.

Математический аппарат метода динамической верификации намного сложнее, чем метод распознавания статической подписи. Он позволяет фиксировать параметры процесса подписи в реальном времени, например, скорость движения руки на разных участках, порядок нанесения штрихов, форму и направление штрихов, силу давления и длительность различных этапов подписи. Это гарантирует, что подпись не подделает даже опытный графолог, поскольку никто не может в точности скопировать поведение руки владельца подписи.

Вот пример

Рис.1 Отмасштабированная оригинальная подпись.

Рис.2 Отмасштабированный обвод подписи. Зависимость Y(t)

На данных рисунках (1,2) видно, что оригинальная подпись и обвод фактически не отличаются друг от друга, а это значит, что распознание статической подписи не надежно.

Процесс динамической верификации подписи происходит в несколько этапов.

Когда мы пишем на планшете, изображение сразу же оцифровывается, и на компьютер передаются координаты полученных точек. Через некоторые равные промежутки времени планшет отправляет на компьютер координату точки, в которой в данный момент находится стилус.

Получаем значения функций.

а) б)

Рис.3 Зависимость Y(t)(а) и усредненная зависимость Y(t)(б)

а) б)

Рис.4 Отмасштабированная оригинальная подпись (а) и восстановленная подпись по усредненным значениям(б)

Разложение в ряды дает возможность не терять чувствительности из-за усреднения и хранить меньшее количество коэффициентов - благодаря использованию вейвлет-разложения функций X(t), Y(t), Z(t)

Получаемая матрица коэффициентов позволяет восстановить исходные функции. Так как вейвлет-коэффициенты сходятся к нулю быстрее, чем коэффициенты разложения Фурье, то при сравнимых объемах данных можно хранить больше информации о подписи.

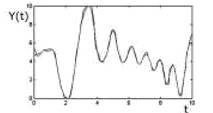
Рис.5 Зависимость Y(t), Аппроксимация Y(t) с помощью ряда Фурье, Аппроксимация Y(t) с помощью вейвлет-разложения.

Структура системы аутентификации в этом случае полностью совпадает со структурой для функционалов Фурье. В качестве эталона в данном случае берется матрица усредненных коэффициентов. При этом можно использовать различные базисы вейвлет-разложений, например, DOG-вейвлет, MHAT-вейвлет; LP-вейвлет, гауссов вейвлет первого порядка.

Математический аппарат вейвлет-преобразований является эффективным методом при решении задач идентификации подписи и почерка. Благодаря достаточно высокой степени развития математических пакетов обработки сигналов, эта задача достаточно легко решается средствами, как платных пакетов, так и пакетов с открытым исходным кодом.