Карачун В.В., Мельник В.М.

Національний технічний університет України «КПІ»

СТУПІНЬ ВПЛИВУ ПРУЖНОЇ ДЕФОРМАЦІЇ ТА ЗМІНИ ГЕОМЕТРІЇ КОРПУСУ АПАРАТА НА ЙОГО ГРАНИЧНІ ПЕРЕМІЩЕННЯ

Обчислимо переміщення циліндричної оболонки (в загальному випадку тіла довільної форми) підводного апарату та РН, поверхня котрих під дією нестаціонарної хвилі надлишкового тиску певним чином деформується. Спочатку розглянемо вимушений рух підводного апарату, потім рух РН в шахтному відсіку.

Попередніх зауважень та обмежень щодо форми збурюючої хвилі констатувати не будемо. Коефіцієнти пружності “с” та демпфірування “b” мають узагальнене значення з урахуванням певної кількості факторів. Наприклад, властивостей тросових систем.

Вимушене переміщення підводного апарату. Лінійність задачі дозволяє навести рівняння руху в проекціях на його центральні осі інерції у вигляді

(1)

де – маса, або момент інерції за наявності кутового переміщення апарату, вважаючи корпус пружно деформуємим тілом довільної форми; – прискорення центру мас (лінійне, або кутове); – сила (чи момент), з якою хвиля, що поширюється в середовищі, діє на абсолютно твердий недеформований корпус;  – додаткова сила (момент) взаємодії оболонки корпусу з водою, яка є породженням деформацій поверхні

(2)

де – тиск, обумовлений переміщенням підводного апарату; – одиничний вектор відповідної осі координат; – координати точки поверхні; – час; – поверхня корпуса апарату.

Залежність узагальненої сили від переміщень поверхні апарату може бути наведена в явному вигляді, для чого досить зобразити їх наступним чином –

(3)

де – достатньо повна система векторних функцій, до речі, при ці функції співпадають з означеними вище , тобто відповідають переміщенням поверхні в цілому, а останні () визначають деформації поверхні; – узагальнена координата.

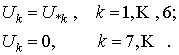
Припустимо, що корпус апарату переміщується, чи деформується, таким чином, що узагальнена координата зростає з одиничною швидкістю, тобто

У цьому разі на поверхні виникає тиск із складовими по всім напрямкам . Співвідношення (2) окреслить узагальнену силу , відповідно до зазначених умов.

За лінійності задачі, узагальнену силу , що виникає при довільному зміщенні поверхні, можна обчислити за допомогою рівності, безпосередньо витікаючої з принципу суперпозиції –

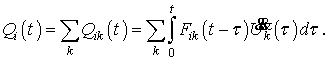(4)

Тут і надалі вважається, що , а в загальному випадку містить імпульсні функції (зокрема, якщо ).

Залежність узагальнених сил від параметрів хвилі тиску також може бути визначена функцією . Отримати таку залежність можна уявленням руху частини рідинного середовища, подумки обмеженого поверхнею корпуса апарату. Динамічну рівновагу отриманого “фіктивного” тіла можна описати рівнянням, аналогічним (1), якщо “фіктивне” тіло при цьому розташоване на місці рухомого апарату, а динамічний стан вивчається відносно обраних вище осей, тоді складові зовнішнього збурення на нестискну поверхню і функції для “фіктивного” тіла будуть такими ж, як і для досліджуємого апарату. З оглядом на сказане, маємо –

(5)

де – маса ( статичний момент, момент інерції “фіктивного” тіла відносно зазначених осей); індекс “Ф” означає належність до “фіктивного” тіла.

Приймемо як твердження, що підводний апарат не відокремлений від середовища, тому в реальній рідині переміщення часток води на поверхні рухомого об’єкту співпадають з переміщенням самого об’єкту. У випадку ідеальної рідини, мова йдеться про нормальні складові переміщень. Момент сил інерції наводиться тут сумою моментів, що виникають внаслідок узагальнених переміщень як при , так і при , оскільки осі, відносно котрих розглядається динамічна рівновага “фіктивного” тіла, не слугують для нього головними центральними осями інерції.

“Фіктивне” тіло не вносить збурень в поширюючуся в середовищі хвилю, тому необхідні дані про його зміщення – , – можуть бути одержані шляхом інтегрування відповідним чином спроектованих зміщень води по поверхні та об’єму апарата. Таким чином, рівняння (5) можна вважати за рівність, яка визначає силу .

Згідно співвідношень (4) та(5), рівняння руху підводного апарату набуває вигляду інтегродиференціального виразу

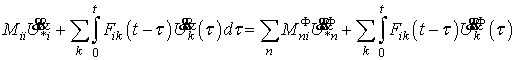. (6)