Технические науки/6.Электротехника и радиоэлектроника
Аринова Н.В.,
Кислинский Р.А., Дарыбаев М.К.
Восточно-Казахстанский
государственный технический университет им. Д.Серикбаева, Казахстан
МОДЕЛИРОВАНИЕ ЭЛЕКТРОФИЗИЧЕСКИХ
СВОЙСТВ СЫПУЧИХ МАТЕРИАЛОВ
Разработка
диэлькометрических высокочастотных влагомеров основывается на использовании
частотно-влажностных характеристик (ЧВХ) измеряемого сыпучего материала.
Получение таких характеристик в широком спектре частот экспериментальным путем
требует много времени и высокой квалификации экспериментатора. При этом необходимо изучить большое число
конкретных образцов сыпучих материалов, охватывающих все возможные комбинации
их характеристик во всем диапазоне изменения их электрофизических свойств [1]. Моделирование
поведения сыпучего вещества в электрическом поле измерительного преобразователя
и получение аналитических выражений компонентов полной проводимости позволяет получать
ЧВХ с учетом физико-механических свойств измеряемого материала в неограниченном
диапазоне частот. Многообразие форм частиц сыпучего материала определяет сложную
структуру смеси, поэтому задача нахождения параметров сыпучего материала аналитическим
методом может быть решена лишь при значительных упрощениях – идеализациях. Реальная
хаотическая структура заменяется упорядоченной ей адекватной структурой. Идеализируя
структуру сыпучего материала можно получить данные, дающие общее представление
об электропроводности в зависимости от различных факторов, учитывающих
физико-механические характеристики сыпучего материала [2].
Идеализированная
упрощенная структура сыпучего материала представлена на рисунке 1. Идеализация определяется следующей системой
допущений:
-
сыпучий материал является гетерогенным двухкомпонентным;
-
частицы 1 и 2 соответственно первого и второго компонентов кубической формы с
размерами ребер а и b, причем ![]() и
и ![]() ;
;
-
распределение влаги по частице равномерное;
-
расположение частиц относительно друг друга и вектора напряженности
электрического поля ![]() показано на рисунке 1;
показано на рисунке 1;
-
сыпучее вещество в момент нахождения его электрических параметров можно
охарактеризовать как капиллярнопористое тело. Между частицами существует некое
поровое пространство, наполненное средой со своими электрофизическими
свойствами, причем пористость структуры сыпучего материала определяется
соотношением геометрических размеров частиц;
-
поверхности частиц в направлении вектора напряженности электрического поля ![]() эквипотенциальны;
эквипотенциальны;
-
линии тока в частицах параллельны в направлении вектора ![]() и распределяются в частицах равномерно.
и распределяются в частицах равномерно.
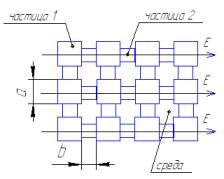
Рисунок
– 1 Способ укладки частиц сыпучего вещества
На основании
принятых допущений разработана математическая модель поведения сыпучего
материала в электрическом поле (аналитическое описание электрических и
диэлектрических параметров сыпучего материала).
Задача математической
модели сводится к определению полной электропроводности конечного объема
сыпучего материала, под которой понимаем интегральное значение этого параметра.
Для получения аналитических выражений воспользуемся
параметрами отдельных частиц. Эти параметры действительны только для одной
отдельно взятой частицы. Условно их можно назвать дифференциальными
параметрами. К ним относятся удельное сопротивление, удельная проводимость,
диэлектрическая проницаемость, микротвердость, плотность, теплоемкость и др.
Для получения
дифференциальных параметров сыпучего материала выделяем участок объема сыпучего
материала, состоящий из двух частиц и зон их контактирования. Участок является системой двух частиц. Графически
система двух частиц представлена на рисунке 2. Частица 2 входит в эту систему
полностью (целиком в виде куба с ребром b). Частица 1 разделена на две одинаковые половины со сторонами а/2 в направлении вектора напряженности
электрического поля ![]() . Такое представление системы двух частиц позволяет
учитывать проводимость частиц и контактных площадок между частицами. Изменение размеров а
и b соответствует изменению гранулометрического состава
сыпучего материала.
. Такое представление системы двух частиц позволяет
учитывать проводимость частиц и контактных площадок между частицами. Изменение размеров а
и b соответствует изменению гранулометрического состава
сыпучего материала.

Рисунок 2 – К расчету полной
проводимости системы из двух частиц
Система частиц разбита на отдельные зоны,
для которых легко определить активную и
реактивную составляющие проводимости простыми методами.
Зоны 1 и 2 на рисунке 2 характеризуются
проводимостями соответственно частиц 1 и 2.
Зона 3 является зоной контакта
двух частиц. Две половины частицы 1 рассматриваем как полную первую зону. Система
двух частиц рассматривается как последовательное их соединение в направлении
вектора ![]() . Каждый участок
соединения представлен в виде активного сопротивления R и емкости С на нулевой и бесконечной частоте для
учета различных видов поляризации сыпучего материала. Для быстро и медленно
протекающих процессов поляризации принимается соответственно параллельная и
последовательная схемы замещения. Эквивалентная электрическая схема замещения
системы двух частиц приведена на рисунке 3.
. Каждый участок
соединения представлен в виде активного сопротивления R и емкости С на нулевой и бесконечной частоте для
учета различных видов поляризации сыпучего материала. Для быстро и медленно
протекающих процессов поляризации принимается соответственно параллельная и
последовательная схемы замещения. Эквивалентная электрическая схема замещения
системы двух частиц приведена на рисунке 3.

Рисунок 3 – Эквивалентная
схема замещения системы двух частиц
Для схемы замещения на рисунке 3 приняты
следующие обозначения:
![]() ,
,
![]() ,
,
![]() и
и ![]() – соответственно активное сопротивление зон 1, 2, зоны контактирования 3
и среды на постоянном токе;
– соответственно активное сопротивление зон 1, 2, зоны контактирования 3
и среды на постоянном токе;![]()
![]() ,
, ![]() ,
, ![]() и
и ![]() – соответственно
дополнительные емкости между собственными поверхностями зоны 1, зоны 2 , площадки контактирования 3 и
между поверхностями разных частиц 1 за
вычетом емкости площадок контактирования 3 на постоянном токе в направлении
– соответственно
дополнительные емкости между собственными поверхностями зоны 1, зоны 2 , площадки контактирования 3 и
между поверхностями разных частиц 1 за
вычетом емкости площадок контактирования 3 на постоянном токе в направлении ![]() ;
;
![]() ,
, ![]() и
и ![]() – соответственно индуктивность зоны 1 и зоны 2 каждой частицы
и индуктивность зоны контактирования 3;
– соответственно индуктивность зоны 1 и зоны 2 каждой частицы
и индуктивность зоны контактирования 3;
![]() ,
,![]() ,
,![]() и
и![]() – соответственно добавочные активные сопротивления зон
1 и 2, площадки контактирования и среды на бесконечной частоте;
– соответственно добавочные активные сопротивления зон
1 и 2, площадки контактирования и среды на бесконечной частоте;
![]() ,
,
![]() ,
, ![]() ,
, ![]() – соответственно емкости
между поверхностями в направлении
– соответственно емкости
между поверхностями в направлении ![]() частицы 1,
частицы 2, зон разных частиц 1 за вычетом
площадки контактирования 3 и площадки контактирования 3 на бесконечной
частоте.
частицы 1,
частицы 2, зон разных частиц 1 за вычетом
площадки контактирования 3 и площадки контактирования 3 на бесконечной
частоте.
При
расчете использованы соотношения:
![]() ,
,![]() ,
,![]() (1)
(1)
где ![]() – удельное
сопротивление материала частицы и зоны контактирования на постоянном токе;
– удельное
сопротивление материала частицы и зоны контактирования на постоянном токе; ![]() – удельное
сопротивление материала частицы и зоны контактирования на бесконечной частоте.
– удельное
сопротивление материала частицы и зоны контактирования на бесконечной частоте.
![]() (2)
(2)
где ![]() – удельное
сопротивление среды на постоянном токе;
– удельное
сопротивление среды на постоянном токе; ![]() – удельное сопротивление среды на бесконечной частоте.
– удельное сопротивление среды на бесконечной частоте.
![]() ,
,![]() ,
,![]() (3)
(3)
где ![]() – диэлектрическая проницаемость материала
частицы и зоны контактирования на постоянном токе;
– диэлектрическая проницаемость материала
частицы и зоны контактирования на постоянном токе; ![]() – диэлектрическая проницаемость материала
частицы и зоны контактирования на бесконечной частоте.
– диэлектрическая проницаемость материала
частицы и зоны контактирования на бесконечной частоте.
![]() ,
, 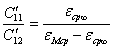 (4)
(4)
где![]() – диэлектрическая
проницаемость среды на постоянном токе;
– диэлектрическая
проницаемость среды на постоянном токе;
![]() – диэлектрическая проницаемость среды на
бесконечной частоте.
– диэлектрическая проницаемость среды на
бесконечной частоте.
Для
расчета величин с одинаковыми первыми индексами использованы величины:
![]() для
для ![]() ,
, ![]() для
для ![]() ,
, ![]() для
для ![]() ,
, ![]() для
для ![]() (5)
(5)
![]() для
для ![]() ,
, ![]() для
для ![]() ,
, ![]() для
для ![]() ,
, ![]() для
для ![]() (6)
(6)
![]() для
для ![]() ,
, ![]() для
для ![]() ,
, ![]() для
для ![]() ,
, ![]() для
для ![]() (7)
(7)
![]() для
для ![]() ,
, ![]() для
для ![]() ,
, ![]() для
для ![]() ,
, ![]() для
для ![]() (8)
(8)
Электрические
параметры элементов в схеме на рисунке 3 определяются через геометрические
размеры частиц и электрофизические свойства материалов и среды. Схема замещения
уточняется и преобразуется в простейшую RC-цепь с параллельным включением
активных потерь в сыпучем материале. В процессе эквивалентных преобразований
схемы замещения получены аналитические выражения R и С. Используя эти
аналитические выражения, получаем расчетные частотно-влажностные характеристики
сыпучих сред с моделируемыми свойствами. Отличительной особенностью данной
математической модели является то, что аналитически описывается поведение в
электрическом поле сыпучей смеси, которая состоит из двух компонент с разными
электрофизическими свойствами, а также учитывается гранулометрический состав
сыпучего материала.
Эти особенности
позволяют расширить применяемость математической модели к анализу различных по
компонентному и гранулометрическому составу сыпучих смесей.
Литература
1.
Кричевский Е.С. Высокочастотный контроль влажности при обогащении
полезных ископаемых. М., «Недра», 1972. - 216 с.
2. Дубров Н.С. и др. Многопараметрические
влагомеры для сыпучих материалов/Н.С.Дубров, Е.С.Кричевский, Б.И.Невзлин. – М.:
Машиностроение, 1980. – 144 с.