Металлургия

Е.В.Максимов, Ж.К.Камбаров, Ю.Б.Ичева

г.Экибастуз, Екибастузский инженерно-технический институт им.академика К.И.Сатпаева

ГОМОГЕНИЗАЦИЯ ЖИДКОЙ ВАННЫ

При продувке жидкой ванны газовыми струями определенный ее объем насыщается газами, что приводит к изменению плотности этого слоя жидкости и вызывает дополнительное перемешивание ванны. Причем, что при продувке ванны появляется отраженный поток газа, а для изучения динамики всплывающей струи рассмотрим трехмерный случай.

     Будем исходить из полной системы уравнений гидродинамики, содержащей уравнение неразрывности

                                                          (1)

уравнение сохранения импульса (Новье-Стокса)

;

;                                 (2)                                    

.

     В нашем случае всплывающая струя отличается от окружающей среды не столько температурой, сколько концентрацией газа. Поэтому вместо уравнения сохранения энергии (уравнение притока тепла) запишем уравнение переноса

;                                                 (3)                                               

Где V(U,V.W) – вектор скорости течения струи; t – время; x,y.z – вектор силы, приходящийся на единицу массы;  - кинематическая вязкость; D – коэффициент молекулярной диффузии газа.

    Следует отметить, что эти уравнения хорошо описывают поведение однородной струи. Однако следует учесть, что секундная масса вдоль струи меняется за счет «подсасывания» массы из окружающей среды [1], вследствие этого подъемная сила частично затрачивается на подъем  не только массы струи, но и добавочной массы окружающей среды. Естественно, что это требует учета движения потока с переменной массой. Поэтому рассмотрим, как изменяются основные уравнения движения при этом.

     Уравнение неразрывности выражает закон сохранения массы, когда скорость увеличения массы металла, содержащейся в данном пространстве, должна быть равна разнице между количествами металла, вытекающими из этого пространства и втекающими в него. Исходя из стандартных рассуждений в отношении массы (но не плотности среды), получим:

или

.

Так как мы принимаем массу за величину переменную, то имеем:

или

  .

Отсюда

 

 + .

Для установившегося процесса

                                               .                                               (4)

Рассмотрим теперь уравнение движения. Второй закон Ньютона в применении к жидкости имеет вид

где  D/Dt – субстанционная производная, ;

 - массовые внешние силы; - поверхностные силы (силы давления и трения).

Исходя из того, что эти силы массовые, получаем:  - силы, действующие на всю массу:

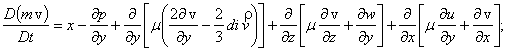
Изменение массы содержится здесь в левой части, рассмотрим этот член подробнее:

Согласно уравнению неразрывности:

или

Таким образом, для установившегося процесса получим:

;

;                    (5)                                                       

.

Полученные уравнения отличаются от обычных, присутствием члена с ln m. Теперь рассмотрим правую часть выражения с учетом уравнения неразрывности:

   (6)

В уравнениях (2) внешние силы x и y можно приравнять нулю. Однако при продувке металла в конвертере, когда его плотность изменяется под воздействием температуры, в поле тяжести действуют архимедовы силы, которые приводят к свободной конвекции. В этой связи, уравнение (1) должно быть уточнено. Внешняя сила, т.е. сила тяжести на единицу массы z = -g, а плотность gотр , как функция температуры, зависит от времени и координат, так как  T= T(x,y,z). Если T = T0 + T1 (где, T0  - среднее значение, а T1 – отклонение от T0), тогда  (где  - постоянная плотность при Т=Т0), а .

Это выражение является уравнением состояния жидкости, где  - коэффициент теплового расширения стали.

Учитывая вклад этих членов ( для Р0 принимаем гидростатическое давление - , получаем Р = Р0 + Р1:

                                            (7)

Плотность окружающей жидкости меняется по высоте вследствие распределения температуры. Так как  - , где Т1 = T  - Т0 - Т0(z) = . Следовательно, разность между температурами струи и окружающего металла есть функция от z:

.

Распределение  считаем заданной функцией.

Отнесём полученные уравнения к задаче всплывания струи, примем

x=y=0;

.

Величину давления (архимедову силу) можно выразить через

или                                                 ,                                             (8)

где  - плотность окружающей среды, - плотность струи; F – площадь поперечного сечения струи; u – продольная составляющая  скорости струи.

При этом  принимаем, что в струе u >>v  и  u>>w. В этом случае масса струи будет составлять

.                                                    (9)

Предположим, что  и вначале упростим задачу, т.е проигнорируем вначале турбулентностью. Тогда вместо скоростей будем иметь усредненные величины

            .                     (10)  

Рассматривая в дальнейшем равномерное смешение  металла по высоте и производя соответствующие преобразования, получим

                                                     (11)

или      .                              (12)                           

     Толщину промежуточного слоя можно определить по следующей зависимости [2]

;                                                            (13)

где V  - скорость течения потока в поперечном направлении.

При исследовании устойчивости сдвигового равновесия разноплостностных  жидкостей в работе [3] рекомендуется следующая формула для учета сил вязкости

                                                          (14)

Использование полученных зависимостей (8), (9), (12), и (13) для расчета толщины промежуточного слоя металла применительно к вышеописанным конкретным условиям показывает, что она составляет  0.47 м.

В работе [4] на основе экспериментальных данных показано, что при относительном движении двух неоднородных по плотности жидкостей между ними возникает пограничный слой, в котором наблюдается непрерывное изменение скорости и плотности. В этом случае определяющими параметрами перемешивания разноплостностных слоев жидкости будут числа Re  и Fr , относящиеся к промежуточному слою. Из анализа размерностей следует, что устойчивость и уровень перемешивания двух слоев жидкости определяется выражением

,                                                                                     (15)

где с – параметр устойчивости; n – постоянная, равная 3/2.

Отсюда скорость перемешивания жидкости  можно определить по следующей зависимости

.                                                       (16)

Таким образом, зная объем промежуточного слоя, его скорость, определяем мощность перемешивания металла.

ЛИТЕРАТУРА

1.Максимов Е.В., Торговец А.К., Изместьева О.А., Продувка жидкой ванны турбулентными закрученными струями. Алма-ата: Галым, 1992,  92 с.

2. Bonlot F., Daubert A. Model mathemtigue de la renionte de la salinite sons une forme stratifice en regime non permanent. XVI tn Congn. Int. Assoc. Hygraul. Res. Kyoto, 1969, vol.3.

3. Clang P.C., Lin A. The Creat salt lake – abiced laboratory for stratified fiov studies. Int. Symp. Stratified Flows. Novosibirsk, 1972.

4. Harleman D.R.F. The turbulent diffusion and convection of sabire watch en idealized estuary. Int. Assoc . of Sei . Hydran l, 1960, publ. 51.