Технические науки / 10. Горное дело

Д. т. н. Тутанов С. К., к.т.н. Тутанов М. С., Тутанова М. С.

Карагандинский государственный технический университет, Казахстан

Устойчивость карьерных бортов с учетом напряженно-деформированного состояния прибортового массива

Борт карьера, как техногенное сооружение, является основным несущим технологическим элементом при открытой разработке месторождений. Поэтому, важной задачей является определение параметров напряженно-деформированного состояния (НДС) массива, влияющие на устойчивость бортов карьера. С элементами уступов по назначению рассматривается вертикальное сечение борта массива горных пород. В качестве расчётной

схемы выбрана прямоугольная плоскость, находящаяся в плоско-деформированном состоянии, и которая разбивается сеткой треугольных элементов, с соответствующими граничными условиями. Задача решается методом конечных элементов (МКЭ) [1].

Для обработки исследований по определению НДС массива горных пород, в частности для определения устойчивых размеров уступов и берм при разработке месторождения, применяется нетрадиционный метод построения многомерных математических моделей [2].

Для того, чтобы получить математическую модель типа y = f(x₁, x₂, x₃, x₄, x₅, x₆), где y – максимальное главное растягивающее напряжение; x₁ = h₁, x₂ = h₂, x₃ = h₃, x₄ = γ₁, x₅ = γ₂, x₆ = Е. исследованы 25 вариантов НДС массива. В каждом варианте решалась задача определения НДС массива МКЭ.

При решении плоской задачи МКЭ изменялись параметры (технологические факторы).

На рисунке 1 приведены изолинии касательных напряжений для одного из вариантов

Изолинии касательных напряжений

Рисунок 1

По вышеуказанной программе получена математическая модель типа, учитывающая комплекс факторов

σ₁^max = f(x₁, x₂, x₃, x₄, x₅, x₆).

В качестве функции выбрана максимальное главное напряжение.

При коэффициенте корреляции R = 0,965, получено обобщенное уравнение следующего вида:

Y(σ₁^max) = Y(h₁)*Y(h₃)*Y(γ₂)*Y(h₂) + Y(E) + Y(γ₁) (1)

где h₁ – высота уступа, Е – модуль упругости, γ₁ – объемный весь верхнего слоя, h₂ – берма, γ₂ – объемный весь нижнего слоя, h₃ – проекция откоса.

По формуле (1), полученной для многомерной модели можно найти комплекс факторов, влияющих на устойчивость бортов карьера.

Зависимости высоты уступа от σ^p_adm

Рисунок 2

Зависимости высоты уступа от γ₁

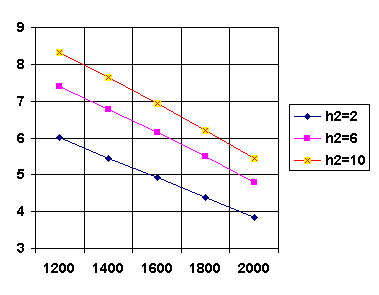
Рисунок 3

По данной зависимости определяется по известным значениям искомая величина из следующего условия прочности горных пород:

σ₁^max ≤ σ^p_adm,

где σ^p_adm – допускаемое растягивающее напряжение

Зависимости высоты уступа от γ₂

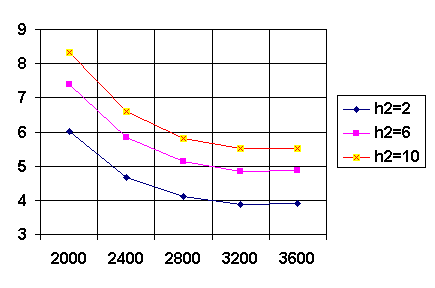
Рисунок 4

На рисунках 2 - 4 приведены графики распределения зависимости высоты уступа от различных факторов. При изменении одной из этих величин значения остальных фиксировались.

Литература

1 Ержанов Ж. С., Каримбаев Т. Д. Метод конечных элементов в задачах механики горных пород. - Алма - Ата: Наука, 1975. - 238 с.

2 Ермеков М. А. , Махов А. А. Нетрадиционный метод построения многомерных моделей на ЭВМ. Караганда, 1990, 30 с.