Технические науки/ 4.Транспорт

УДК 629.3.081.3

М.А. Камалян, С.А. Кузнецов

Южно-Российский государственный университет экономики и сервиса, Россия

Автомобильный тормоз новой конструкции

Разработана конструкция автомобильного тормозного механизма, сочетающего в себе высокую эффективность со стабильностью коэффициента эффективности [1]. Высокая стабильность в этой конструкции достигается за счет отсутствия самоусиления, равно как и самоослабления, по аналогии с дисковыми тормозными механизмами, в которых также отсутствует самоусиление. С другой стороны, возможность создания как самоусиления, так и самоослабления любой величины при необходимости конструкцией допускается. Кинематика тормоза, представляющего собой центроидный зубчато-планетарный механизм, оригинальна тем, что колодка радиуса r совершает вынужденное (не самоустанавливающееся) движение огибания по отношению к барабану, радиус R которого больше на величину эксцентриситета е. Наличие дополнительной высшей пары, образованной взаимоогибаемыми элементами колодки и барабана, позволяет отнести тормоз в структурном плане к механизмам с избыточной связью, или индифферентным механизмам.

накладка

Рис. 1 - Схема конструкции центроидного тормоза

Индифферентность структуры проявляется в том, что замыкающее усилие в фрикционной паре барабан-колодка не приводится к входному звену в виде уравновешивающего момента, если точка приложения силы F совпадает с теоретической точкой контакта Р (рис.1). В общем случае результирующая взаимодействия колодки с барабаном F проходит через точку контакта К и смещена относительно теоретической точки контакта Р на угол α, так как между взаимоогибаемыми поверхностями имеется фрикционная накладка. Ориентировочно точка приложения К реактивной силы взаимодействия F, определяемой толщиной накладки и создаваемым ею натягом, находится на дуге, ограничивающей пятно фрикционного контакта. Реальное положение точки контакта К приложения результирующей взаимодействия F зависит от многих геометрических и силовых факторов, в том числе от приработки фрикционной пары, поэтому для ее уточнения необходимо провести эксперимент.

Коэффициент эффективности определяется как отношение момента тормозного М_тр к моменту приводному М_пр, приложенному к входному звену, либо приведенному к радиусу барабана приводному усилию [2].

Момент торможения М_тр можно определить как произведение силы трения в паре барабан-колодка на радиус R барабана:

(1)

где μ – коэффициент трения фрикционной накладки о барабан радиуса R.

Момент приводной силы М_пр определяется как момент, приведенный от силы F взаимодействия барабана и колодки:

где F_пр можно определить из теоремы Жуковского:

В относительном движении подвижной и неподвижной центроид точка Р является мгновенным центром скоростей, поэтому расстояние между ней и точкой К приложения взаимодействующей двух взаимоогибаемых дуг радиусов R и r пропорционально скорости v_k точки К, в то время как скорость v_a точки А пропорциональна радиусу r.

После замены скоростей их аналогами с учетом того, что аналоги скоростей являются плечами соответствующих сил, то есть перпендикулярны им, приведенная сила:

Из прямоугольного треугольника РON определяем плечо РN:

Таким образом, в соответствии с теоремой Жуковского приведенная к водилу сила равна:

,

а момент приводной:

(2)

Коэффициент эффективности с учетом (1) и (2):

,

где F- усилие общей нормали; μ – коэффициент трения; R – радиус барабана; r – радиус колодки; e=R-r – длина водила, или эксцентриситет приводного звена.

В конечной формуле две неизвестных величины – угол β и коэффициент эффективности К_э. Если определить коэффициент эффективности экспериментально, то можно вычислить и угол β:

.

Задача дальнейшего исследования состоит в определении положения точки К относительно пятна фрикционного контакта, то есть в определении взаимосвязи между параметрами пятна контакта и углом β.

Изготовлен экспериментальный образец такого тормоза и испытан на стенде с двигателем постоянного тока, в котором момент тормозной определяется через потребляемый ток, пропорциональный моменту [3]. Нагружение входного звена производится путем воздействия на рычаг силой тяжести.

Момент торможения определялся из пропорции:

С учетом потерь холостого хода

,

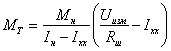где сопротивление шунта .

Испытания показали, что коэффициент эффективности нового тормоза равен К_Э=6, то есть в 20 раз больше, чем у дискового тормоза, если коэффициент эффективности дискового тормоза равен, как известно, коэффициенту трения μ = 0,3 (одной колодки).

В экспериментальном образце приняты следующие параметры внутреннего зацепления зубчатого колеса колодки и неподвижного зубчатого венца: z₁ = 100; z₂ = 106 (такие числа зубьев приняты из условия отсутствия интерференции зубьев); при этом делительные диаметры для зубьев, нарезанных без смещения исходного контура, для принятого модуля m=1,5 равны d₁ = 150 мм; d₂ = 159 мм. Отсюда радиус колодки , радиус барабана отличается от делительного радиуса зубчатого венца на 0,5 мм: с этим небольшим различием связано расхождение коэффициента эффективности при реверсировании двигателя экспериментальной установки. Почти полное совпадение моментной характеристики при реверсировании также свидетельствует об отсутствии самоусиления, то есть о высокой стабильности тормозного момента и коэффициента эффективности (рис.2).

τ

Рис. 2 – Экспериментальная моментная характеристика при реверсировании двигателя

С учетом параметров экспериментального образца определяем угол смещения теоретической точки контакта β:

.

Обследование пятна контакта притертой колодки показало, что такой угол соответствует угловой длине пятна контакта, которая зависит от толщины накладки, причем, чем тоньше накладка (точнее, перекрытие накладки относительно образующей барабана), тем больше коэффициент эффективности, что, впрочем, закономерно. С другой стороны, при определении расчетного значения коэффициента эффективности угол β следует принимать равным углу геометрического перекрытия образующих накладки и барабана. Для этого можно из геометрических соображений определить угол α, который является угловым размером притертой части фрикционной накладки и немного больше угла β.

Угол α определяется как точка пересечения окружности радиуса R и окружности радиуса r+δ, описанного из точки, отстоящей на величину эксцентриситета е от центра окружности радиуса R. Для определения угла α примем следующую расчетную схему (рис.3).

Эксцентриситет, то есть длина водила, для данных параметров определяется по формуле:

.

Перекрытие тормозной накладки относительно образующей барабана обозначено на схеме (рис.3) как δ; от этого параметра зависит усилие прижатия колодки к барабану. В треугольнике АОК известны длины всех сторон, поэтому угол γ определяется по формуле [4]:

, где полупериметр

поскольку

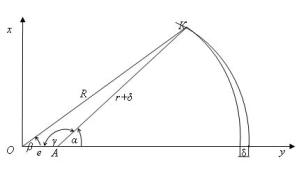
Рис.3 – Расчетная схема для определения углов α и β

Угол α определяется как дополняющий к γ:

.

Угол β определяется по формуле:

.

Например, для данных параметров механизма при величине перекрытия около 0,9 мм величина углов α и β оказывается соизмеримой с полученным выше экспериментальным значением.

Список литературы

1. Колодочный тормоз: Патент РФ №2188345, М. Кл.⁴ F 16 D 51/00, 51/16 / С.А. Кузнецов, М.А. Камалян (РФ)

2. Мащенко А.Ф., Розанов В.Г. Тормозные системы автотракторных средств.- М.: Транспорт, 1972. -144 с.

3. Камалян, М.А. Стенд для испытания автомобильного тормоза: Межвуз. научн.сб / М.А. Камалян, С.А. Кузнецов.-Шахты: Изд-во ЮРГУЭС, 2006.- С. 43-44.

4. Корн Г., Корн Т. Справочник по математике. – М.: Наука, 1977.- 832 с.