Удк 621.365.51

Головащенко П.Д.

Національний технічний університет України

«Київський політехнічний інститут»

КОМП’ЮТЕРНЕ МОДЕЛЮВАННЯ ІНДУКЦІЙНОЇ КАНАЛЬНОЇ ПЕЧІ

З ОБЕРТОВИМ РУХОМ РІДКОГО МЕТАЛУ

Аналіз досліджень та постановка задачі. Обертовий рух рідкого металу знаходить широке застосування в різноманітних технологічних процесах металургійного та ливарного виробництв, де він дозволяє в одних випадках інтенсифікувати технологічний процес, в інших – реалізувати принципово новий процес, який неможливо отримати у відсутності такого руху. Особливо перспективним в цьому відношенні є його використання в електроплавильному обладнанні, наприклад, в індукційних канальних печах. Слід зазначити, що значимість такого обладнання в цьому випадку значно зростає в зв’язку зі зміною за останній час концепції плавки металів. Якщо донині економічно вигіднішим для цього було використання, наприклад, газових печей, а ніж електричних (електроплавлення в основному використовується в регіонах з дешевою електроенергією, наприклад, в Сибірському регіоні Росії), то нині в зв’язку з різким подорожчанням органічних енергоносіїв, в т.ч. природного газу, картина змінюється на зворотну. Особливо актуальним це стає для України, яка змушена імпортувати газ по високим цінам, маючи в той же час лишки електричної енергії у себе.

За даними досліджень наявність в індукційних канальних печах обертового руху рідкого металу дозволяє вирішити декілька важливих технологічних задач, як-то: інтенсифікувати тепло- і масообмін між індукційними каналами і ванною печі, зменшити “заростання” каналів окислами, реалізувати безпосередньо в печі очищення (рафінування) розплаву від неметалевих домішок за рахунок їх коагуляції.

Виклад основного матеріалу. На рис.1 наведено ескізне зображення індукційної канальної печі (точніше основної її частини – так званої “індукційної одиниці”, що стикується з ванної печі), яка служить для плавлення алюмінію і його сплавів. Як відомо, індукційна канальна піч в електромагнітному відношенні подібна електричному трансформатору, первинна обмотка (індуктор) якого живиться від електричної мережі (пічного трансформатора), а вторинна виконана у вигляді короткозамкнутого витка рідкого металу. Короткозамкнутий виток (канальна частина) цієї печі має два циліндричні канали круглого перерізу, що сполучаються між собою двома з’єднувальними каналами, поперечний переріз яких має прямокутну форму. Зазначені канали сформовано керамічним футеруванням в окремих блоках, каркаси яких виконано із немагнітної сталі. Між собою ці каркаси електрично ізольовані один від одного. Наведення електричного струму в рідкому металі канальної частини печі здійснюється за допомогою індуктора з замкнутим магнітопроводом (осердям). В даному випадку розглядається магнітопровод броньового типу.

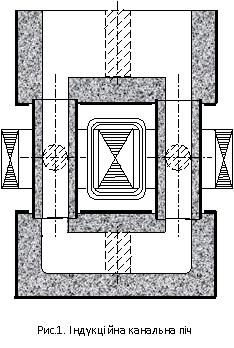
Обертовий рух металу в циліндричних каналах печі створюється електромагнітною системою, яка включає в себе штатний індуктор печі і допоміжну котушку. Котушка має дві намотані поверх індуктора секції, зустрічно з’єднаних між собою. В цій котушці протікає струм, який по відношенню до струму індуктора має фазовий кут, що складає 90 ел. град. За рахунок цього в області обох циліндричних каналів магнітне поле індуктора (поле розсіювання) і магнітне поле допоміжної котушки зсунуті між собою в просторі і в часі на 90 град., що призводить до виникнення в каналах обертового електромагнітного моменту.

Математична модель печі. Важливо вміти розраховувати електромагнітне поле в такій печі з врахування руху рідкого металу в каналах, оскільки це дозволяє визначити як електромагнітні, так і електродинамічні параметри печі, такі як електромагнітний момент і швидкість руху рідкого металу. В роботі [1] задачу розрахунку поля в такій печі розв’язували методом інтегральних рівнянь з врахуванням обертового руху рідкого металу в каналах на основі залучення емпіричного співвідношення для колової швидкості металу, яке було отримане на фізичній моделі печі. Такий метод розрахунку дає непогані результати, але має обмежене застосування, оскільки потребує проведення додаткового фізичного моделювання.

Мета цієї роботи полягає в розробленні математичної моделі індукційної канальної печі з обертовим рухом рідкого металу на основі рівнянь квазістаціонарного електромагнітного поля і рівнянь руху металу та визначення її електродинамічних параметрів. В роботі формулюється і розв’язується задача розрахунку електромагнітного поля печі в плоско-паралельному наближенні (в площині, що проходить поперек циліндричних каналів) разом з диференціальними рівняннями гідродинаміки (рівняннями Нав’є-Стокса).

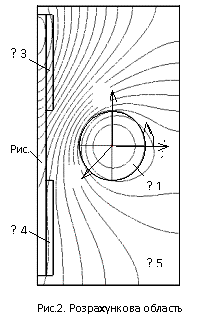
На рис.2 представлено розрахункову область печі, точніше системи “індуктор з допоміжною котушкою – рідкометалевий виток”. Оскільки така система має симетрію відносно осі індуктора, поле розглядається в одній її половині. Крім цього, для спрощення задачі із розгляду вилучені конструктивні електропровідні елементи печі (металеві каркаси циліндричних і з’єднувальних каналів). Вважається також, що магнітна проникність феромагнітного матеріалу магнітопроводу нескінченно велика і тому він також не розглядається. Таким чином, розрахункова область на рис.2 обмежена контуром, що проходить по внутрішній поверхні однієї половини феромагнітного осердя, на якому задається гранична умова . Ця область включає в себе підобласті циліндричного каналу Ω1, індуктора Ω2, допоміжної котушки Ω3 і Ω4, а також підобласть футерувального матеріалу та навколишнього середовища Ω5.

Електромагнітне поле в такій системі у випадку живлення індуктора та допоміжної котушки від джерел змінного струму і при заданій швидкості руху рідкого металу можна описати системою інтегро-диференціальних рівнянь для єдиної компоненти векторного магнітного потенціалу (далі ) і рівняння балансу напруги для рідкометалевого витка відносно наступних невідомих: потенціалу і струму в рідкометалевому витку (струму в каналі) .

Рівняння для векторного потенціалу:

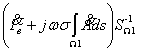– в області Ω1; (1)

– в області Ω2; (2)

- в області Ω3 і Ω4 (3)

– в області Ω5. (4)

Рівняння балансу напруги для рідкометалевого витка: . (5)

В цих рівняннях Гн/м, – питома електропровідність рідкого металу, – кутова частота, і – число витків індуктора і допоміжної котушки (однієї секції), , і – довжини (в напрямку осі z) індуктора, котушки і циліндричного каналу відповідно, (n = 1, …, 4) – площа відповідної підобласті, – активний опір індуктора, – активний опір котушки (двох послідовних секцій), – опір циліндричного каналу постійному струму, – сумарний повний опір обох з’єднувальних каналів, які знаходили попередньо на основі розв’язування додаткових польових задач у відповідності з роботою [2].

Виразивши із рівняння (5) струм і підставивши його в (1), отримаємо наступний вираз для правої частини рівняння (1), що має розмірність густини струму: . (6)

Розв’язання рівнянь (1) – (4) з врахуванням виразу (6) при заданій швидкості дозволяє отримати розподіл параметрів електромагнітного поля (індукції магнітного поля , густини струму та ін.) в циліндричному каналі печі (в області Ω1), що дає можливість розрахувати електромагнітні сили, які виникають в рідкому металі, , (7)

де – спряжений комплекс індукції магнітного поля.

Для визначення швидкості рідкого металу залучали рівняння гідродинаміки у вигляді рівнянь Нав’є-Стокса з k-ε моделлю турбулентності ; (8)

, (9)

де – густина рідкого металу, – тиск, і – коефіцієнти кінематичної і турбулентної в’язкості металу відповідно.

Згідно з k-ε моделлю турбулентності коефіцієнт турбулентної в’язкості визначають як , (10)

де – емпірична константа, – густина кінетичної турбулентної енергії, – швидкість її дисипації. Останні параметри зв’язані між собою та швидкістю двома диференціальними рівняннями, які розв’язують разом з рівняннями (8) і (9).

Гідродинамічна задача розглядалась для області Ω1 (див. рис.2), тобто розраховували швидкість руху рідкого металу в поперечному перерізі циліндричного каналу. Граничну умову на стінці каналу при цьому задавали у вигляді логарифмічного профілю швидкості для пограничного шару.

Результати моделювання. Чисельний розрахунок електромагнітної задачі (рівняння (1)–(4)) і гідродинамічної задачі (рівняння (8)-(9)) виконували сумісно в магнітогідродинамічній постановці з використанням програмного пакета мультифізичного моделювання Femlab [3].

Розрахунок проводили для печі, наведеної на рис.1, при наступних вихідних даних: рідкий метал – алюміній ( = 3,6∙10⁶ Ом^-1∙м^-1, = 2,4∙10³ кг∙м^-3, = 10^-6 м²∙с^-1), = 2π·50 с^-1, діаметр циліндричного каналу – 0,19 м, число витків індуктора = 32, сила струму в індукторі – = 1700 А (ефективне значення), число витків допоміжної котушки (однієї секції) – = 20. В якості незалежних змінних виступали сила струму в котушці (модуль) і фазовий кут . Повний сумарний опір обох з’єднувальних каналів, отриманий в результаті розв’язання додаткових польових задач у відповідності з роботою [2], для цієї печі склав: Ом.

На рис.2 наведено картину електромагнітного поля у вигляді ізоліній векторного магнітного потенціалу в розрахунковій області для = j1000А ( = 1000А, ψ = 90 ел. град.) Поява допоміжної котушки в індукційній канальній печі вносить несиметрію в розподіл поля відносно осі x, що позначається також на електромагнітних силах, що розвиваються в рідкому металі. Векторні поля електромагнітних сил в поперечному перерізі циліндричного каналу показано на рис.3. Рис.3а відноситься до випадку = 0, а рис.3б – до = j1000А. Під дією електромагнітних сил в каналі виникає вихровий рух рідкого металу (рис.4). У випадку, коли струм у допоміжній котушці відсутній ( = 0), в поперечному перерізі циліндричного каналу утворюється двоконтурна вихрова течія (рис.4а). З