Карачун В.В., Мельник В.Н.
Национальный технический университет Украины «КПИ»
ИЗГИБНОЕ
ДВИЖЕНИЕ ПЛОСКОЙ ПРЕГРАДЫ В РЕВЕРБЕРАЦИОННОМ ПРОСТРАНСТВЕ
Проведем численный анализ изгибных колебаний теневой
стороны пластины положив для конкретности – ![]() ;
; ![]() ;
; ![]() (алюминиевый сплав Д1 (0);
(алюминиевый сплав Д1 (0); ![]() . Генерируемые в пластине
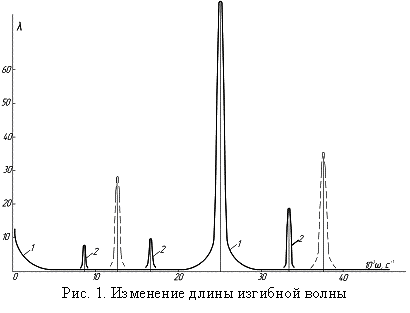
колебания оценим по величинам амплитуды и длины изгибной волны (рис. 1).
. Генерируемые в пластине
колебания оценим по величинам амплитуды и длины изгибной волны (рис. 1).
Если по оси ординат отложить величину длины волны ![]() генерируемых на теневой стороне пластины изгибных колебаний,
а по оси абсцисс –
величину
генерируемых на теневой стороне пластины изгибных колебаний,
а по оси абсцисс –
величину ![]() круговой частоты, то
график, например, при угле
круговой частоты, то
график, например, при угле ![]() примет вид непрерывной
кривой сложной конфигурации, но симметричной относительно оси
ординат (рис. 1, кривая 1) и имеющей
характерные «всплески». В промежутках между ними,
на частотах
примет вид непрерывной
кривой сложной конфигурации, но симметричной относительно оси
ординат (рис. 1, кривая 1) и имеющей
характерные «всплески». В промежутках между ними,
на частотах ![]() и
и ![]() , величина длины волны будет монотонно убывать. Очевидно, что
средняя мощность процесса распределяется неравномерно по частотам
, величина длины волны будет монотонно убывать. Очевидно, что
средняя мощность процесса распределяется неравномерно по частотам ![]() падающей звуковой волны в
пределах от нуля до
падающей звуковой волны в
пределах от нуля до ![]() . Так, на частотах
. Так, на частотах ![]() равных
равных ![]() ,
, ![]() ,
, ![]() в спектре наблюдается
наложение двух форм колебаний различной амплитуды и протяженности
(кривые 2). Пунктирная линия на рис. 1 изображает значения длин
модулирующих волн основных изгибных колебаний. Это явление
наблюдается на частотах
в спектре наблюдается
наложение двух форм колебаний различной амплитуды и протяженности
(кривые 2). Пунктирная линия на рис. 1 изображает значения длин
модулирующих волн основных изгибных колебаний. Это явление
наблюдается на частотах ![]() , равных
, равных ![]() ,
, ![]() и
соответствует прохождению резонансных областей.
и
соответствует прохождению резонансных областей.
С увеличением угла ![]() падения
звуковой волны спектр изгибных колебаний становится более
насыщенным, усложняется их форма. Диаграмма как бы «сжимается» по оси частот.
падения
звуковой волны спектр изгибных колебаний становится более
насыщенным, усложняется их форма. Диаграмма как бы «сжимается» по оси частот.
На частоте ![]() фаза колебаний изменяется на
фаза колебаний изменяется на ![]() .
.
Амплитуда прогиба
пластины с возрастанием частоты ![]() убывает по экспоненциальному закону, но с
увеличением угла падения
убывает по экспоненциальному закону, но с
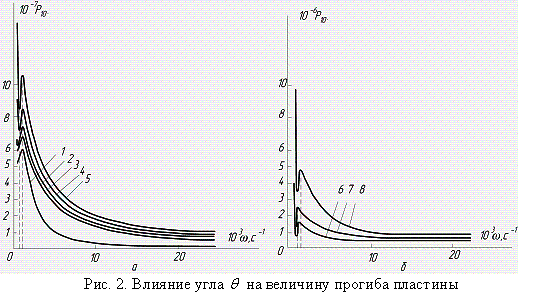
увеличением угла падения ![]() существенно растет по абсолютному значению
(рис. 2). Объяснение этому факту состоит в усилении влияния антисимметричной
составляющей, приводящей к «раскачке».
Интенсивное движение пластины способствует более мощной трансляции звуковой
энергии из одного полупространства в другое.
существенно растет по абсолютному значению
(рис. 2). Объяснение этому факту состоит в усилении влияния антисимметричной
составляющей, приводящей к «раскачке».
Интенсивное движение пластины способствует более мощной трансляции звуковой
энергии из одного полупространства в другое.
Плоская волна является, в некотором смысле, идеализированной схемой
явления. Более приближенным к натурным условиям представляется диффузное поле, когда вероятность
падения звуковой волны одинакова для всех значений угла ![]() .
Проведя несложную операцию осреднения по Пэрису,
.
Проведя несложную операцию осреднения по Пэрису,
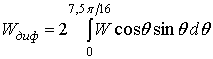 ,
,
можно
установить закон изгибного движения пластины при равновероятностном переносе
звуковой энергии.
Численный анализ говорит о том, что при прочих равных условиях, в диффузном
поле амплитуда изгибной волны с увеличением частоты ![]() также уменьшается по экспоненциальному
закону.
также уменьшается по экспоненциальному
закону.
Быстрота уменьшения
более значительная на частоте ![]() ,
причем происходит с одновременным изменением фазы колебаний на
,
причем происходит с одновременным изменением фазы колебаний на ![]() .
.
Для решения целого
ряда задач необходимо знать степень влияния частоты ![]() на
коэффициент
на
коэффициент ![]() отражения звука (рис.
3). На диаграмме
отражения звука (рис.
3). На диаграмме
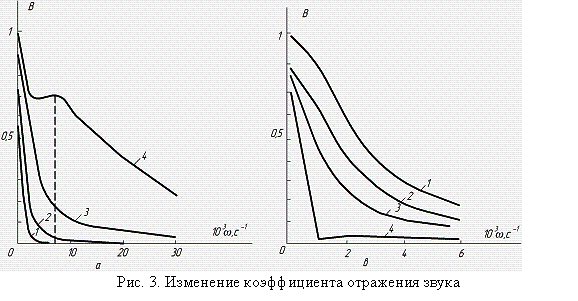
представлены его значения для
разных толщин пластины (рис. 3, а), а также для различных углов ![]() падения волны (рис. 3, б).
падения волны (рис. 3, б).
На рис. 3, а приняты следующие
обозначения графиков: ![]() м;
м; ![]() м;
м; ![]() м;
м; ![]() м.
м.
На
рис. 3,
б обозначено: ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.