Технические науки/3. Отраслевое машиностроение

К.т.н. Гольдштейн Ю.М.

Институт технической механики НАН и НКА Украины, Украина

К вопросу использования кластерного анализа в
функциональном диагностировании сложных
технических систем

Системы функционального диагностирования применяют при использовании объекта по назначению, когда необходимы проверка правильности функционирования и поиск дефектов, нарушающих последнее. При этом на объект поступают только предусмотренные его алгоритмом функционирования (рабочие) воздействия.

Успешное решение диагностических задач в значительной мере обусловлено удачным выбором информативных диагностических признаков и алгоритмов распознавания.

Состояние объекта описывается множеством определяющих его параметров. Распознавание состояния объекта представляет собой отнесение объекта к одному из возможных классов (диагнозов).

Часто требуется провести выбор одного из двух диагнозов: «исправное состояние» или «неисправное состояние». В большинстве задач технической диагностики диагнозы (классы) устанавливаются заранее, и в этих условиях задачу распознавания часто называют задачей классификации.

В задачах диагностики сложные технические системы описывается с помощью комплекса признаков, и могут характеризоваться - мерным вектором или точкой в - мерном пространстве, причем координаты могут быть количественными, порядковыми или качественными.

Как правило используются два основных подхода к задаче распознавания: вероятностный и детерминистский.

Вероятностный подход является более общим, но он требуют значительно большего объёма исходной информации о диагностируемой технической системе. Поэтому его практическое использование имеет существенные ограничения для сложных и уникальных технических систем.

Для таких систем более применимы детерминистские методы диагностики. При детерминистских методах распознавания удобно формулировать задачу на геометрическом языке. Если объект характеризуется - мерным вектором, то любое состояние объекта представляет собой точку в - мерном пространстве параметров (признаков). Предполагается, что диагноз соответствует некоторой области рассматриваемого пространства признаков. Требуется найти решающее правило, в соответствии с которым вектор (диагностируемый объект) будет отнесён к определённой области диагноза. Таким образом, задача сводится к разделению пространства признаков на области диагнозов.

Области диагноза представляют собой внутренне однородные и внешне изолированные группы (кластеры). Для их определения во многих случаях целесообразно использовать методы кластерного анализа.

Кластерный анализ дает возможность производить разбиение объектов не по одному параметру, а по ряду признаков. Кроме того, кластерный анализ в отличие от большинства математико-статистических методов не накладывает никаких ограничений на вид рассматриваемых объектов и позволяет исследовать множество исходных данных практически произвольной природы.

Решением задачи кластерного анализа являются разбиения, удовлетворяющие критерию оптимальности. Этот критерий может представлять собой некоторый функционал, выражающий уровни желательности различных разбиений и группировок, который называют целевой функцией. В задачах функциональной диагностики в качестве целевой функции удобно выбрать внутригрупповая сумма квадратов отклонений:

,

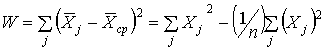где - вектор показателей - го состояния технической системы, - средний вектор показателей. В качестве меры сходства между состояниями технической системы принимается расстояние между ними (чем меньше расстояние, тем состояния более схожи).

Следует отметить, что в результате применения различных методов кластеризации и используемых расстояний могут быть получены кластеры различной формы. Поэтому выбор метода кластеризации играет существенную роль.

В задачах функционального диагностирования сложных технических систем обычно заранее известно количество классов (диагнозов), к которым нужно отнести систему.

Для решения задач такого типа целесообразно использовать метод - средних. Алгоритм случайным образом в пространстве показателей назначает центры будущих кластеров. Затем вычисляет расстояние между центрами кластеров и каждым объектом, и объект приписывается к тому кластеру, к которому он ближе всего. Завершив приписывание, алгоритм вычисляет средние значения для каждого кластера. Этих средних будет столько, сколько используется переменных для проведения анализа, - штук. Набор средних представляет собой координаты нового положения центра кластера. Алгоритм вновь вычисляет расстояние от каждого объекта до центров кластеров и приписывает объекты к ближайшему кластеру. Вновь вычисляются центры тяжести кластеров, и этот процесс повторяется до тех пор, пока центры тяжести не перестанут «мигрировать» в пространстве показателей.

Использование некоторого априори известного разбиения пространства показателей на кластеры диагнозов (обучающего множества) и современных быстродействующих пакетов программ (например “Statisyica-7”) позволяют оценить качество разбиений на кластеры при использовании различных методов кластеризации и расстояний и подобрать их оптимальный вариант.