Экономические науки/12.Экономика сельского хозяйства

К.э.н. Сазонова Д.Д.

Всероссийский научно-исследовательский институт использования техники и нефтепродуктов в сельском хозяйстве Россельхозакадемии, Россия

Методика оптимизации аллокативной эффективности

фермерских хозяйств

Анализ аллокативной эффективности позволяет судить о том, является ли использование того или иного ресурса избыточным, оптимальным или недостаточным при сложившихся ценах на рынке ресурсов и конечной продукции, а также доступном уровне для данной совокупности производителей технологий и организации производства продукции [1-4]. Для оценки аллокативной эффективности использования i-того ресурса применяется функция предельного продукта (предельной (маржинальной) производительности ресурса), которая представляет собой первую частную производную функции по этому ресурсу и показывает, на сколько единиц увеличится результирующая переменная Y, если объем затрат этого ресурса возрастет на одну единицу (достаточно малую) при неизменных объемах остальных ресурсов.

В случае функции Кобба-Дугласа предельный продукт i-того ресурса опишется зависимостью:

, (1)

где - средние значения постоянных ресурсов (j ≠ i).

Определим значение предельного продукта при среднем значении ресурса. Умножив правую часть равенства (1) на дробь , получим

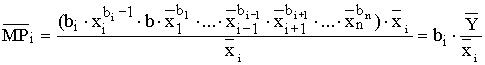, (2)

то есть предельный продукт i-того ресурса при данном (среднем) его значении пропорционален средней производительности с коэффициентом b_i.а среднюю пр равен коэффициента ем)на предельного продлукта у ресурсу и

Так как в правой части равенства (1) все члены, кроме x_i, постоянны и имеют определенные значения, то функцию предельного продукта i-того ресурса можно записать в следующем виде:

, (3)

где

. (4)

Этот постоянный множитель рассчитан как произведение средних значений постоянных факторов x_j (j≠i) в соответствующей степени, свободного члена производственной функции b и показателя степени переменного ресурса i, то есть тех составляющих формулы (1), которые являются постоянными и не зависят от величины переменного фактора x_i.

В общем виде оптимальные значения ресурсов определяются решением задачи на максимум прибыли:

PR= Y – Z ® max, где - функция затрат.

Значение ресурса x_i, при котором функция прибыли PR примет максимальное значение, определится решением уравнений:

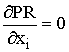Þ Þ 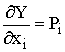Þ MP_i =P_i (5)

Производственная функции, представленная в виде функции Кобба-Дугласа, при равенстве прочих ресурсов средним своим значениям сводится к функции одной переменной , где значение d_i определено равенством (4). Производственная функция, приведенная к такому виду, обладает рядом специфических условий: в частности, 0<b_i<1, значения ресурса x_i неотрицательны, с ростом затрат ресурса растет значение результирующей переменной (Y), причем каждая дополнительная единица ресурса x_i обеспечивает все меньший прирост Y, и, следовательно, графиком производственной функции является кривая, которая напоминает выпуклую вверх «горку», крутизна которой падает. Функция затрат при условии, что прочие ресурсы постоянны и равны своим средним значениям, принимает вид:

(6)

Тогда решением уравнения (5) будет являться точка . Поскольку полученная критическая точка является единственной, то она является точкой максимума прибыли.

Таким образом, оптимальное значение переменного ресурса х_i (при условии, что значения остальных ресурсов постоянны и зафиксированы на средних уровнях) удовлетворяет равенству МР_i=Р_i, где Р_i - стоимость единицы i-того ресурса. Если в производственной функции ресурс представлен не в физическом, а в денежном исчислении, то, естественно, последнее уравнение будет иметь вид МР_i=1.

Значения ресурса х_i, удовлетворяющие неравенству МР_i>P_i (кривая предельного продукта, согласно рисунку 1, выше прямой, соответствующей стоимости ресурса P_i, и, соответственно, ), свидетельствуют о недоиспользовании ресурса: увеличение ресурса приведет к увеличению прибыли. Значения ресурса х_i, удовлетворяющие неравенству МР_i < P_i , свидетельствуют об избыточном использовании ресурса: прибыль можно увеличить уменьшением использования ресурса.

Задача определения ресурсного обеспечения, при котором все ресурсы, входящие в производственную функцию, аллокативно эффективны, сводится к нахождению максимума производственной функции при равенстве предельных продуктов ресурсов их стоимостям.

(7)

при условии

(8)

Рисунок 1 - Кривые прибыли и предельного продукта i-того ресурса

Решение этой задачи методом Лагранжа дает единственную точку. Полученная критическая точка является точкой условного локального (также глобального) максимума функции (7) при системе ограничений (8).

Литература

1. Farrel J. Michael (1957): The measurement of Productive efficiency. Journal of the Royal Statistical Society. Series A, General 125 Part 2: 252-267

2. Рынок покупных ресурсов в российском сельском хозяйстве // Научные труды ИЭПП №63Р – М.: ИЭПП,2003,с.29-31

3. Эпштейн Д. Аллокативная эффективность использования ресурсов сельхозпредприятиями // АПК: экономика, управление, №3, 2006, с.39-42

4. Сазонова Д.Д., Сазонов С.Н. Аллокативная и техническая эффективности фермерских хозяйств – М.:МОНФ, 2010. – 159с.