Економічні науки/ 8. Математичні методи в економіці

Савчук А.В.

Науковий керівник: асистент Настасій О.Б.

Буковинська державна фінансова академія, Україна

Застосування методів диференціального числення до дослідження попиту на еластичність

Дуже часто економісти в своїх розрахунках застосовують похідну для обчислення різноманітних виразів, функцій. Одним із найпоширеніших методів застосування похідної є обчислення еластичності попиту, яка є дуже важливою для підприємств різної галузі. Для того, щоб знати попит на готову продукцію будь-якому підприємцю треба знати яка еластичність цього попиту, на скільки попит змінюється відносно зміни інших факторів виробництва і піддається цим факторам.

Нехай р – вартість одного виробу, а х – кількість виробів, що виготовлена та продана за деякий певний інтервал часу. Позначимо залежність між кількістю проданого товару і його вартістю x=f(p).

Позначимо еластичність попиту через ῆ

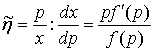, (1)

де dx, dp позначають приріст кількості товару і приріст ціни за одиницю даного товару відповідно.

Дамо пояснення еластичності попиту ῆ. Якщо вартість виробу змінилась на ∆ р, тобто р +∆ р − «нова» ціна, тоді і кількість виробів також зміниться на величину ∆х = f (р+∆ р) − f (р). Відносний приріст вартості буде , а відносний приріст функції попиту . Якщо відносний приріст помножити на 100, то одержимо відповідний відсоток зміни початкової вартості та початкового попиту [1,с 233].

Наприклад, початкова вартість одного виробу – 2 гривні зросла до 2,10 гривні, тоді ∆ р = 2,1 – 2 = 0,10 гривні. Отже, відносна вартість = 0,05 вказує на зростання початкової вартості. Якщо цю величину помножити на 100%, то одержимо відсоток зміни початкової вартості кожного виробу:

100% × = 100 * 0,05 = 5%

Аналогічно 100× дорівнює відсотку зміни початкового попиту. Якщо зростання вартості викликає спад попиту, тоді ∆х < 0.

Розглянемо відношення відносного приросту попиту до відносного приросту вартості одиниці продукції:

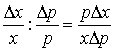. (2)

Це співвідношення показує в скільки разів відносний приріст попиту більше відносного приросту вартості виробу. Якщо в останній рівності перейти до границі при ∆ р →0, то одержимо:

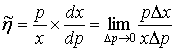. ( 3)

Оскільки границя ῆ відрізняється від виразу на нескінченно малу більшого порядку малості відносно ∆ р→0, ῆ≈, або: відсоток зміни попиту ≈ῆ.

Наприклад, якщо зростання вартості на 2% викликає спадання попиту на 3%, тоді еластичність попиту буде ῆ = = . Якщо еластичність попиту ῆ = −1,5, тоді 2% зростання вартості викликає зміну попиту на (−1,5) × 2% = -1% [4,с 294]

Зазначимо, якщо відсоток зміни попиту більше відсотка вартості (ῆ<−1), тоді попит називають еластичним; якщо відсоток зміни попиту менше відсотку зміни вартості (-1<ῆ< 0), тоді попит називають не еластичним. Якщо ῆ= −1, то попит називають адекватним вартості одиниці виробу.

Поняття еластичності можна застосувати не тільки для випадку функцій, що описують попит, але і до інших функцій економічного змісту.

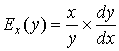, (4)

де − деяка задана функція.

Ця еластичність є наближений відсоток приросту функції (зростання або спадання), відповідний приросту незалежної змінної на 1%. Таким чином, будь-який суб’єкт виробництва визначає рівень попиту на свою готову продукцію при цьому враховуючи його еластичність.

ЛІТЕРАТУРА:

1. Барковська Н.В., Барковський В.В., Вища математика для економістів . – Київ :ЦУЛ, 2002.- 400с. – серія: Математичні науки.

2. Грисенко М.В., Математика для економістів: Методи й моделі , приклади й задачі: Навч. посібник. – К. Либідь, 2007. – 720с.

3. Дубовик В.П., Юрик І.І.,Вища математика:Навч. посібник. – К.: Видавництво А.С.К., 2004. – 648с.

4. Дюженкова Л.І., Дюженкова О.Ю., Михалі Г.О., Вища математика: Приклади і задачі / Посібник. – К.: Видавничий центр «Академія», 2003. – 624с.

5. Травкін Ю.І., Малярець Л.М., Математика для економістів: Підручник. – Х.: ВД «ІНЖЕК» 2005. – 816с.