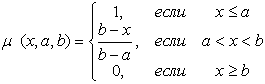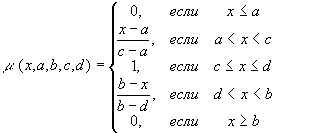Д.т.н., проф. Димитров В.П., д.т.н., проф. Борисова Л.В.

Донской государственный технический университет, Россия

К вопросу о представлении нечетких экспертных знаний

При построении интеллектуальных информационных систем поддержки принятия решений в сфере эксплуатации сложных машин широко используются базы знаний, основанные на нечетких знаниях, т. е. нечеткие продукционные системы [1]. Поэтому одним из актуальных является вопрос представления нечеткой экспертной информации. Блок приобретения и корректировки знаний является одним из основных блоков интеллектуальных информационных систем (экспертных систем).

Нечеткая экспертная информация трудноформализуема в рамках традиционных математических формализмов. Для описания признаков предметной области «технологическая регулировка зерноуборочных комбайнов» эксперты могут применять разные множества их лингвистических значений. В одном случае возникают трудности в связи с недостаточностью значений, в другом в связи с их избыточностью. В результате чего следует ожидать увеличения нечеткости и рассогласованности поступающей от экспертов информации. Естественным вопросом при оценивании экспертом проявлений признаков является вопрос: «По каким критериям должен производиться выбор оптимального множества значений лингвистической шкалы, которая применяется при оценивании того или иного признака?».

Описание критериев оптимальности выбора значений лингвистических переменных в [2] содержит следующие требования: а) минимальная неопределенность для экспертов при описании реальных объектов; б) максимальная согласованность экспертной информации.

Важной практической задачей является определение оптимального множества значений лингвистических переменных, используемого для оценивания факторов внешней среды, регулируемых параметров машины и показателей качества работы.

Для адекватного представления нечеткой экспертной информации о предметной области необходимо установить оптимальное число термов (m₀) лингвистической переменной (ЛП), учитывая ограничения снизу inf m₀ и сверху sup m₀. Сверху число термов ограничено соображениями точности измерения рассматриваемого параметра. Например, для лингвистической переменной «засоренность хлебной массы» эта точность не может быть высокой, а, следовательно, число термов не может быть большим. Если же выбрать число термов слишком малым, то затруднено выявление и описание взаимодействий данного фактора с показателями качества работы (такой случай приводит в вырождению данной зависимости). При решении рассматриваемой задачи целесообразно проводить оценку согласованности нечетких экспертных знаний.

Рассмотрим в качестве примера случай, когда 5 экспертов дали оценки функций принадлежности для 3-х термов («низкая», «средняя», «высокая»), для 4-х термов («низкая», «средняя», «высокая», «очень высокая») и 5-и термов («очень низкая», «низкая», «средняя», «высокая», «очень высокая»). Пример используемых функций принадлежности и значения параметров приведены в таблицах 1 и 2.

Номер эксперта будем обозначать индексом i = 1, 2, …, k. а номер терма – индексом l = 1, 2, …, m. Функцию принадлежности, которую задал i-й эксперт для l-го терма, обозначим .

Таблица 1 – Вид функций принадлежности

Вид терма	Выражение для ФП
Левый терм
Центральные термы
Правый терм
	Область определения для x от 0 до 1 (нормированные значения). Область определения для a, b, c, d от 0 до 1.

Таблица 2 – Значения коэффициентов a, b, c, d функций принадлежности

для различных экспертов

3 терма	Значения параметров ФП для различных экспертов
Вид терма	1 эксперт	2 эксперт	3 эксперт	4 эксперт	5 эксперт
Левый	a = 0,04 b = 0,16	a = 0,07 b = 0,20	a = 0,04 b = 0,14	a = 0,03 b = 0,15	a = 0,08 b = 0,19
Центральный	a = 0,04 b = 0,36 c = 0,16 d = 0,24	a = 0,07 b = 0,38 c = 0,20 d = 0,24	a = 0,04 b = 0,30 c = 0,14 d = 0,18	a = 0,03 b = 0,38 c = 0,15 d = 0,24	a = 0,08 b = 0,40 c = 0,19 d = 0,26
Правый	a = 0,24 b = 0,36	a = 0,24 b = 0,38	a = 0,18 b = 0,30	a = 0,24 b = 0,38	a = 0,26 b = 0,40

При анализе согласованности нечеткой экспертной информации вначале вычисляются аддитивный и мультипликативный показатели общей согласованности, а потом по их величинам формулируется суждение о согласованности моделей экспертного оценивания. Затем строится матрица парной согласованности моделей X_i и X_j экспертов.

Показатель различия между моделями двух экспертов, i-го и j-го, в рамках l-го терма определяется как линейное расстояние (Хемминга) между нечеткими множествами с функциями принадлежности и [2].

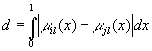. (1)

Показатель согласованности между этими же моделями определяется величиной k_ij:

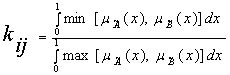. (2)

На основе матрицы парной согласованности моделей для всех термов находится матрица согласованности моделей X_i и X_j по всем термам. Ее элементы определяются формулой:

, (3)

где m – число термов.

Нами рассмотрена задача определения выражений (1) и (2) для различных вариантов взаимного расположения функций принадлежности и .

В качестве примера приведены условия для для центральных термов.

На тех интервалах, где ==1 или ==0, подинтегральная функция в формуле (1) равна 0. Из интервала [0, 1] интегрирования остаются следующие участки:

а) одна из функций или тождественно равна 1, а другая является линейно убывающей или линейно возрастающей.

б) обе функции и являются линейно возрастающими или линейно убывающими.

в) одна из функций или тождественно равна 0, а другая является линейно возрастающей или линейно убывающей.

г) одна из функций и является линейно возрастающей, а другая линейно убывающей.

д) одна из функций или тождественно равна 0, а другая равна 1.

Результаты расчетов аддитивных и мультипликативных показателей по формулам (1) представлены в таблице 3.

Таблица 3 – Результаты расчета показателейи

Модель
3-х термовая	0,655	0,628
4-х термовая	0,542	0,503
5-и термовая	0,509	0,460

Анализ значений полученных показателей общей согласованности экспертной информации показывает, что наиболее согласованной является 3-х термовая модель, менее согласована 4-х термовая и еще менее – 5-и термовая. При этом различие в степени согласованности 4-х и 5-и термовых моделей незначительно.

В результате анализа различных вариантов расположения функций принадлежности выявлены типовые случаи, для которых получены выражения для расчета коэффициентов нечеткости и согласованности. Полученные результаты использованы при разработке алгоритмов модификации в подсистеме ввода нечетких экспертных знаний интеллектуальной информационной системы для технологической регулировки машин.

Литература

1. Борисова Л.В., Димитров В.П., Тугенгольд А.К. К вопросу построения нечеткой экспертной системы продукционного типа для технологической регулировки машин/ Вестник ДГТУ, Т.8 № 3 (38), 2008. С. – 278 – 287.

2. Обработка нечеткой информации в системах принятия решений/А.Н. Борисов, А.В. Алексеев, Г.В. Меркурьев и др.–М.: Радио и связь, 1989.– 394 с.