Белушенко В.С., Шмаков Ю.Д.

Национальный Горный Университет, г. Днепропетровск, Украина

Использование стохастических моделей для оперативного контроля напряженно-деформированного состояния породного массива.

Для эффективного управления горными объектами, а также для повышения безопасности работ и предотвращения катастрофических явлений, в мире существуют сложные и весьма дорогостоящие системы геомеханического мониторинга (СГМ), представляющие собой автоматизированные информационно-измерительные системы непрерывного контроля, диагностики и прогноза напряженно-деформированного состояния (НДС) породного массива, осуществляемых с целью повышения уровня безопасности при строительстве, эксплуатации и закрытии размещенных в его пределах искусственных сооружений.

Выполнение перечисленных задач в полном объеме возможно только с использованием автоматизированных систем геомониторинга на основе современной компьютерной техники и соответствующего программно-аппаратного обеспечения. Одной из важнейших задач, решаемой в рамках СГМ, является осуществление оперативной диагностики НДС той части породного массива, которая недоступна для визуальных наблюдений. При этом, обычно анализируется детерминированная составляющая пространственной неоднородности массива – тренд, описывающий (на данном масштабном уровне) изменения значений показателей массива, например, в зоне повышенных напряжений или в зоне упрочнения. Выделение тренда в массиве вокруг горной выработки является основной задачей при контроле напряженного состояния или процесса упрочнения массива. [1]

Среди геофизических методов, успешно применяемых для прогноза НДС породного массива, наиболее эффективными являются акустические методы, поскольку они информативны, технологичны и позволяют оперативно контролировать напряженное состояние той части породного массива, которая недоступна для визуальных наблюдений без нарушения его сплошности [2].

При использовании методов акустического контроля состояния пласта обычно применяются методы диагностики, суть которых заключается в посылке в пласт зондирующих акустических сигналов и приеме вернувшихся из породного массива сигналов с последующим их анализом, на основе которого делается вывод о состоянии массива. Поскольку при этом свободные или вынужденные колебания возбуждаются только в части породного массива, то эти методы диагностики также классифицируются как локальные, обеспечивающие оперативную диагностику только определенной части массива. Сигналы, принятые из породного массива и подлежащие последующей обработке, будем в дальнейшем называть информационными сигналами.

Наиболее приемлемыми для задач оперативной диагностики НДС породного массива оказались методы, использующие вынужденные колебания, возникающие в пласте при взаимодействии с ним шахтных механизмов (комбайн, буровое оборудование, отбойный молоток и т.п.) в процессе их работы. Это обеспечивает практически непрерывный контроль состояния породного массива в окрестностях области выполнения работ. Недостатком этих методов является недетерминированность зондирующих акустических сигналов, обусловленных работой шахтного оборудования, так как они существенно зависят от режима работы оборудования. Это осложняет последующий анализ информационных сигналов.

В результате разрушения угольного пласта под действием шахтных механизмов в породном массиве возникают упругие колебания, которые, по сути, и представляют собой зондирующий сигнал. Будем считать, что зондирующий сигнал имеет спектр S_з(jω), где ω – циклическая (круговая) частота (ω = 2 π f), f - спектральная компонента (частота), а j – мнимая единица.

На рис. 1 представлена структурная схема формирования информационного акустического сигнала.

Зондирующие сигналы проходят через призабойную область породного массива, которая относительно этих сигналов может рассматриваться как акустический фильтр с передаточной функцией K_м(jω). Пройдя через угольный пласт, упругие колебания попадают во вмещающие породы, которые достаточно “прозрачны” для них. В этой связи их затуханием во вмещающих породах обычно пренебрегают. В таких породах обычно пробуривается шпур, в который устанавливается геофон, преобразующий эти колебания в электрический сигнал, который и является входным (информационным) сигналом для электронной обрабатывающей аппаратуры системы геомониторинга. Если амплитудно-частотная характеристика (АЧХ) геофона описывается передаточной функцией K_г(jω), то спектральный состав сигнала на выходе геофона S_г(jω), может быть определен по формуле:

S_г(jω) = S_з(jω) K_м(jω) K_г(jω). (1)

Следует отметить, что непосредственная регистрация зондирующего сигнала невозможна. Поэтому во многих случаях априори предполагается, что этот сигнал имеет шумовой характер, т.е. имеет равномерно распределенные спектральные компоненты f в определенной полосе частот. Поскольку характеристики сигнала на выходе геофона могут быть измерены непосредственно, а характеристики самого геофона известны, то при априорно известных характеристиках зондирующего сигнала по этим данным можно получить акустическую передаточную функцию породного массива:

K_м(jω) = S_г(jω) / [S_з(jω)∙K_г(jω)]. (2)

Следует отметить, что хотя возможен и непосредственный расчет по формуле (2), на практике обычно переходят от спектральных представлений к частотным характеристикам, которые могут быть легко получены при обработке акустических сигналов аналоговыми методами.

Именно этот принцип и был положен в основу аппаратуры акустического контроля АК-1 [3], разработанной в Днепропетровском горном институте. Установленная взаимосвязь между АЧХ распространяющихся в массиве упругих колебаний и уровнем возникающих в нем напряжений позволили определить комплексный показатель выбросоопасности К. При его определении с помощью активных аналоговых фильтров выделяются амплитуды составляющих спектра акустических колебаний в высокочастотной A_в и низкочастотной A_н областях спектрального диапазона сейсмоакустического сигнала. По отношению этих величин и судят об уровне выбросоопасности.

Непрерывность характера контроля НДС углепородного массива основана на том, что текущие показания комплексного показателя выбросоопасности К линейно изменяются во времени и отражают изменения напряженности исследуемой области в реальном масштабе времени. Пределы изменения показателя К колеблются в интервале от 0 (для неопасной с точки зрения выбросоопасности) до 5 и более (непосредственно перед внезапным выбросом угля и газа) условных единиц. Применительно к проблеме прогноза внезапных выбросов угля и газа показания аппаратуры АК-1 используют как индикатор превышения критического уровня (К = 3), сигнализирующего о вхождении в опасную зону.

В состав системы геомониторинга входят внешние датчики наблюдательных станций, устанавливаемые в толще пород контролируемого массива (подземный полукомплект) и наземный полукомплект, обеспечивающий прием и окончательную обработку поступающих сейсмоакустических сигналов.

Из теории систем известно, что вид передаточной функции K_м(jω) определяется ее коэффициентами. Так как акустические свойства породного массива зависят от его состояния [2], то можно считать, что коэффициенты функции K_м(jω) также характеризуют состояние массива и могут быть использованы для его оценки.

На практике типичны ситуации, когда основным источником информации о поведении объекта являются данные измерений наблюдаемой величины, сделанных в последовательные моменты времени - временные ряды. Создание моделей по экспериментальным временным рядам в математической статистике и теории автоматического управления получило название идентификации систем, а в нелинейной динамике - реконструкции динамических систем.

Существует два подхода к разработке моделей систем. Наиболее проверенный и надежный путь - записать модельные уравнения, исходя из гак называемых «первых принципов» (общих законов для данной облает явлений, таких как законы сохранения, законы Ньютона в механике, уравнения Максвелла в электродинамике, и т.п.) с учетом особенностей объекта.

Второй подход заключается в эмпирическом моделировании. Сейчас, когда стали доступны высокопроизводительные компьютеры, сформировалась концепция динамического хаоса, и стало ясно, что сложное поведение может описываться и достаточно простыми нелинейными моделями, он переживает второе рождение. Зачастую такой подход является единственно возможным.

Сигналы, поступающие с подземного полукомплекта на блок обработки сигналов, являются, по сути, временными рядами. Анализ временных рядов (теория обработки сигналов) - обширная прикладная дисциплина, которая включает в себя множество методик и подходов.

Методы, основанные на построении моделей, исторически и логически делятся на две больших группы:

1) Построение линейных стохастических моделей (самый популярный их вид - модели авторегрессии и скользящего среднего). Это направление получило специальное название "идентификации систем". Оно опирается на методы параметрического спектрального анализа[4].

2) Построение нелинейных динамических моделей (как правило, отображений или обыкновенных дифференциальных уравнений). Оно во многом опирается на идеи и методы нелинейной динамики. Поэтому получило свое название: "реконструкция динамических систем".

Эти методы предполагают наличие некоторой статистической модели случайного сигнала. Процесс спектрального анализа в данном случае включает в себя определение параметров этой модели, и потому такие методы называются параметрическими. Используется также термин “модельный спектральный анализ”.

Следует отметить, что поскольку состояние породного массива меняется с течением времени, то очевидно, что и эти коэффициенты функции K_м(jω) подвержены изменению во времени. Поэтому, отслеживание динамики изменения этих коэффициентов во времени, с увязкой ее к реальному состоянию массива, позволит извлечь дополнительную информацию о процессах, происходящих в породном массиве. Поэтому модель должна быть адаптивной. Использование адаптивных методов идентификации систем, позволяет получать информацию о параметрах системы в условиях, когда невозможно получить полную информацию об устройстве системы путем прямого доступа к ней.

Рассмотрим возможность использования таких систем для идентификации параметров углепородного массива. Поскольку имеющаяся информация об идентифицируемом процессе (процессе образования колебаний в породном массиве и формирования акустического сигнала) неполна и не слишком достоверна, идентификация, т. е. получение недостающей априорной информации, должна основываться на самонастраивающейся модели [5] (рис. 2). Будем рассматривать породный массив как некий идентифицируемый объект (или процесс), обладающий некоторой передаточной функцией, коэффициенты которой известны не полностью или недостоверны. Допустим, что на основе некоторой априорной информации, нами разработана некоторая математическая модель, которая с определенной степенью достоверности отражает структуру породного массива. Если на вход идентифицируемого объекта подать информационный сигнал и его же подать на вход модели, то на выходе объекта (процесса) появится выходной сигнал , а на выходе модели – сигнал . Если сравнить эти два сигнала, то сигнал рассогласования

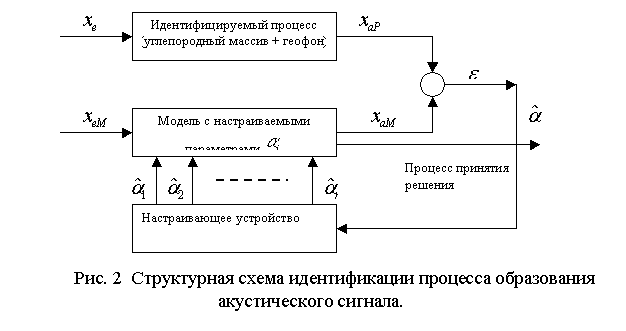
= - (3)

будет характеризовать степень несоответствия модели идентифицируемому объекту (процессу). Самонастройка модели заключается в модифицировании ее параметров , которое осуществляется, например, по минимуму критерия качества .

Однако, поскольку в реальных условиях нельзя получить информацию о входном сигнале , то единственным наблюдаемым параметром идентифицируемого процесса является выходной сигнал , снимаемый с геофона. Для решения проблемы на вход модели необходимо подается тестовый сигнал с параметрами, максимально приближенными к параметрам входного (зондирующего) сигнала. Для этого необходимо уточнить модель формирования этого сигнала.

Описанный способ идентификации позволяет моделировать процесс формирования сейсмоакустического сигнала путем подбора параметров модели , а также тестового входного сигнала .

Сопоставляя полученные параметры модели с известным НДС породного массива, можно определить совокупность значений параметров, соответствующих выбросоопасному состоянию породного массива. При изменении значения НДС от неопасного к опасному, происходит изменение свойств сигналов (временных рядов), поступающих на блок обработки сигналов, что может быть выявлено в процессе обработки информационного сигнала [6].

ЛИТЕРАТУРА

1. Масленников Е. В. Шмаков Ю. Д. Задачи создания аппаратуры акустического контроля в системе геомониторинга породного массива / Науковий вісник НГУ. — Днепропетровск, 2006. – № 9, с. 69-74.

2. Ямщиков В.С. Волновые процессы в массиве горных пород: Учебник для вузов. – М.: Недра, 1984. 271 с.

3. Мирер С. В., Масленников Е. В., Хмара О. И. Метод и аппаратура для акустического контроля выбросоопасности угольных пластов // Внезапные выбросы угля и газа, рудничная аэрология: Научн. сообщ. ин-та горного дела им. А. А. Скочинского. – М.: 1988. – с.20-24.

4. Марпл-мл. С. Л. Цифровой спектральный анализ и его приложения. - М., Мир, 1990. – 584 с.

5. Шульце К.-П., Реберг К.-Ю. Инженерный анализ адаптивных систем. - М., Мир, 1992

6. Обнаружение изменения свойств сигналов и динамических систем / Под ред. М. Бассвиль, А. Банвениста. – М.: Мир, 1989. – 278 с.