Информационная безопасность

ктн, доцент Василенко В. С.

Національний авіаційний університет (НАУ), Україна

Код умовних лишків в задачах контролю та поновлення цілісності

В [1-3] досить детально проаналізовано можливості та основні способі (механізмі) застосування узагальненого коду умовних лишків (ЛУ – коду) в задачах захисту цілісності інформаційних об’єктів телекомунікаційних мереж. Нагадаємо, що теоретичною основою (ЛУ – коду) є система лишкових класів (СЛК). Причому при використанні в завадостійкому кодуванні СЛК в класичному вигляді чи у вигляді коду умовних лишків (ЛУ – коді) [1] постає традиційна для задач цього класу проблема розрізняння невикривлених (правильних) кодових комбінацій (чисел, базових кодових слів) від викривлених (неправильних). Нагадаємо також, що цих системах кодова комбінація (базове кодове слово) розглядається як деяке (реальне в СЛК чи умовне в ЛУ – коді) число. В цих кодах для завадостійкого кодування, як і в інших кодах, вводиться надлишковість у вигляді реального чи умовного лишку від розподілу вихідного числа А на контрольну основу p_k (чи q). Її введення призводить до розширення діапазону представлення до величини , де – діапазон представлення невикривлених чисел (робочий діапазон), а (і = 1, 2, …, n) – основи системи числення, обрані для даної системи представлення. В зазначених умовах не викривленими числами вважаються (цілісність яких ніяким чином не порушена) такі, величина яких не перевищує визначеного наперед діапазону представлення не викривлених чисел (робочого діапазону). Викривлені числа (цілісність яких тим чи іншим чином є порушеною), на відміну від не викривлених, зосереджені за межами робочого діапазону, тобто > Р.

Виявлення факту наявності чи відсутності порушень цілісності в числі (інформаційному об’єкті), тобто виявлення виходу чи не виходу такого числі за межі робочого діапазону – задача відповідних алгоритмів контролю цілісності інформаційних об’єктів. Зрозуміло, що однією із умов можливості побудови таких алгоритмів є коректність (правильність) вибору його констант, якими, в цьому випадку є основи системи числення. Ці основи повинні відповідати певним вимогам. Розглянемо ці вимоги.

Що стосується вибору основ, які створюють робочий діапазон, то вимога до них одна – ці основи повинні бути взаємно простими числами. Вимоги ж щодо надлишковості, яка визначається величиною контрольної основи q, витікають із наступних міркувань.

При виборі величин контрольної основи в задачах контролю та поновлення цілісності будемо враховувати одержані в [1, 2] підходи та результати. Отже, для виявлення наявності спотворень досить визначити, в якому із діапазонів (робочому чи контрольному) знаходиться число, правильність якого перевіряється. Покажемо, що при правильному виборі контрольної основи цього достатньо і для визначення місця і величини такого спотворення.

Спотворене число може бути представленим як сума початкового (не спотвореного) числа А та вектору спотворень Е: , де вектор спотворення Е в СЛК має лишки, що дорівнюють нулю, по усім основам, окрім тієї, де є спотворення. Надалі нагадаємо, що вектор спотворення є числом виду , чи оскільки тільки числа, які діляться націло на мають у своєму представленні в СЛК такий набір лишків. В останніх виразах величина – контрольний (повний) діапазон представлення чисел в СЛК.

На числовій осі величина спотворення відображається точкою в деякому піддіапазоні “контрольного” діапазону [(Р + 1), R). Відповідно, процес спотворення початкового числа А відобразиться переміщенням точки А із робочого діапазону [0, P) в деякий піддіапазон із номером k. Звернемо увагу на те, що в піддіапазон із цим номером k спотворене число (А^/ = l_i×R_i + А₁ чи А^/ = l_i×R_i + А₂) може попасти (див. рис. 1) в залежності від величини початкового числа (А₁ чи А₂) та взаємного розташування лівих границь піддіапазонів – відповідно точок k×Р та l_i×R_i.

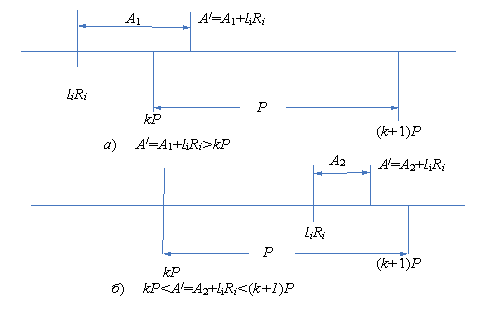
Рис. 1. Ілюстрація розташування спотворених чисел

На рис. 1а зображена ситуація, коли величина початкового числа А₁ перевищує різницю між значеннями l_i×R_i та k·P, тобто коли А₁ > (k·P – l_i×R_i). Ситуація, зображена на рис. 1б відповідає варіанту, коли величина початкового числа А₂ є меншою ніж різниця між значеннями l_i×R_i та (k+1)·P.

В обох випадках величина спотворення (чи довжина вектору спотворення) Е відповідає умові:

(k–1)·P < Е = l_i×R_i < (k+1)·P. (1)

Звернемо увагу на те, що цей же результат може бути одержаним залежно від величини початкового (неспотвореного) числа А при попаданні вектора спотворення Е в межі діапазону, ширину якого можна визначити із виразу (1), якщо від правої частини цього нерівняння відняти ліву:

ΔЕ = (k+1)·P – (k–1)·P = 2P.

Отже правильний результат при декодуванні можна одержати лише у випадку, коли можливі викривлення (чи кінці вектору викривлень) є рознесеними на величину, яка є не меншою ніж ΔЕ = 2P. Оскільки кількість піддіапазонів P в межах контрольного діапазону R = P·p_k визначається величиною контрольної основи (точніше, дорівнює) p_k, то і відстань між кінцями вектору викривлень залежить від величини p_k. Цей висновок повинен бути врахованим при визначення величини контрольної основи p_k.

Із наведеного витікає, що механізми визначення наявності, місця виникнення та величини викривлення повинні ґрунтуватися на виявленні тим чи іншим шляхом хоча б однієї із таких взаємно пов’язаних величин як і, , та, відповідно, , , , . Із наведеного витікає також, що для ідентифікації викривленого числа (чи величини викривлення) із номером основи і слід забезпечити попадання викривлених по різним основам чисел в різні діапазони, що, в свою чергу, є можливим при умові, що відстань між двома довільними діапазонами, в які можуть потрапити викривлені числа, перевищувала б подвійне максимальне значення не викривленого числа (2Р). Наприклад, при
> :

>+ P, чи – > 2P. (2)

Звідси:

– > 2P,

– > 2,

,

.

Оскільки шукане значення контрольної основи (мінімально можливе (граничне) значення) повинно перевищувати величину, яка визначається дробовим числом, то для пошуку максимального значення цієї дробової величини слід визначити максимальне значення чисельника та мінімальне значення знаменника. Максимальне значення чисельника в цьому виразі дорівнює подвійному добутку двох найбільших із основ системи числення , а мінімальне значення знаменника (це цілочисельна величина!):

,

оскільки дорівнювати нулю знаменник може лише тоді, коли

,

що, в свою чергу, є досяжним лише при , а , і що є неможливим (нагадаємо, що основи системи числення, наразі це величини , є взаємно простими числами). Отже, в разі визначення величини та місця викривлення по факту попадання викривленого числа до інтервалу , вимога до мінімально можливого (граничного) значення величини контрольної основи може бути записаною у вигляді:

. (3)

При зворотному співвідношенні між величинами векторів викривлення, тобто при < , їх різниця є від’ємною величиною, тобто – < 0, тоді за правилами виконання модульних операцій (у цьому випадку за модулем R) умова (2) набуде вигляду:

<+ P, чи R + – > 2P.

Звідси:

R + – > 2P,

+ – > 2,

,

.

Як і в попередньому випадку, максимальне значення чисельника в цьому виразі дорівнює подвійному добутку двох найбільших із основ системи числення , а мінімальне значення знаменника (це цілочисельна величина!):

може бути досягнутим при мінімальному значенні другого (позитивного) доданку та максимальному значенні третього (відмінного) – . Не важко побачити, що min (при ), а max() = (– 1) = (при ). Тоді:

min,

а вираз для визначення шуканого максимального значення набуває вигляду:

і є меншим, ніж у виразі (3).

Отже, оскільки правильний результат декодування потрібен у будь-якій ситуації, мінімально можливі (граничні) значення величини контрольної основи слід розраховувати, виходячи із виразу (3).

Таким чином, в статті розглянуті питання визначення величин основ коду умовних лишків для випадків його використання для контролю та поновлення цілісності та запропоновано вирази для розрахунку мінімально можливих (граничних) значень величин контрольної основи.

1. Василенко В.С. Код умовних лишків в задачах контролю цілісності. / В.С. Василенко // Матеріали VІ міжнародної Науково – практичної конференції “Aknualne problemy nowoczenych nauk – 2010” 07–15 червня 2010. Nowoczesne informacyjne technologie.Fizyka– Перемишль: “Nauka I studia” 2010. –Т. 28, С. 34–36; 2. Василенко В.С. Вибір величини контрольної основи для коду умовних лишків. / В.С. Василенко, О.Я. Матов // К.: Реєстрація, зберігання і обробка даних. - 2010. - том 12, № 1. с. 73 – 78.