Химия и химические технологии / 5. Фундаментальные проблемы создания новых материалов и технологий

^*Белевцова Т.В., к.х.н. ^*Бондарев Н.В., к.х.н. ^**Зайцева И.С.

^*Национальный университет имени В.Н. Каразина, Харьков, Украина

^**Харьковская национальная академия городского хозяйства, Украина

Метод констант равновесий

и термодинамика химических превращений

Актуальной задачей теории химических равновесий является выявление термодинамических закономерностей химических превращений в различных средах с целью прогнозирования выхода продукта реакции и управления химическим процессом.

Цель данной работы – рассмотреть основные источники ошибок определения энтальпии (энтропии) химического равновесия эмпирическим дифференцированием и изложить основы регрессионного анализа температурной зависимости констант равновесия для оценки стандартных термодинамических характеристик химического превращения.

Зная температурную зависимость константы равновесия можно рассчитать не только стандартную энергию Гиббса процесса D_rG^o = –RT ln K, но и оценить другие термодинамические параметры – энтальпию D_rН^o, энтропию D_rS^o и теплоемкость D_rС^о реакции, например, с помощью уравнения Вант-Гоффа ln K = A + B/T – для равновесий комплексообразования или Харнеда-Робинсона ln K = A₁/Т + A₂ + A₃T – для равновесий диссоциации. Это крайне важно в тех случаях, когда прямым калориметрическим экспериментом определить D_rН^o невозможно (низкая растворимость реагентов, небольшие скорости процессов). В то же время нахождение термодинамических характеристик реакции из температурной зависимости константы равновесия (методом констант равновесия) сопряжено с серьезными экспериментальными проблемами точности нахождения D_rН^o и D_rS^o, обусловленными общим температурным интервалом (Т₂ – Т₁) проведения эксперимента и ошибками определения констант равновесия при разных температурах (табл. 1 и 2).

Таблица 1. Точность определения D_rH^o с учетом ошибки dK в константе равновесия и температурного интервала

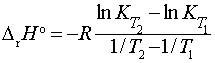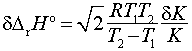, [1]

	dlgK	T2 – T1		кДж/моль
0.05	±0.02	50	300^2	±1.1
		25		±2.2
		10		±5.3
0.10	±0.05	50	300^2	±2.1
		25		±4.2
		10		±10.6

Таблица 2. Точность определения D_rS^o с учетом ошибки dK в константе равновесия и температурного интервала

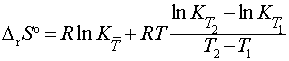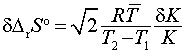, [1]

	dlgK	T2 – T1		Дж/(моль·К)	кДж/моль
0.05	±0.02	50	300	±3.5	±1.1
		25		±7.0	±2.1
		10		±17.6	±5.2
0.10	±0.05	50	300	±7.0	±2.1
		25		±14.1	±4.2
		10		±35.2	±10.5

В работе предложен подход (на примере экспериментальных констант устойчивости комплексов 18С6 с катионами калия K⁺ + L = LK⁺ в водно-пропан-2-ольных растворителях [2]) к оценке точности термодинамических характеристик комплексообразования (табл. 3), основанный на регрессионном анализе температурной зависимости констант равновесия; оценке значимости уравнения регрессии по критерию Фишера; оценке значимости коэффициентов регрессии по критерию Стьюдента; табличном и графическом анализе остатков, подтверждающем адекватность модели и нормальное распределение остатков (показатель Кука, расстояния Махаланобиса).

Значимость уравнения регрессии lg K = A + B/T для аппроксимации температурной зависимости констант равновесия подтверждена F–критерием дисперсионного анализа (F_набл > F_кр)

F_набл = ( r² /k ) / [(1 – r²)/( n–k–1)]

при проверке выполнимости нулевой гипотезы H₀: A =0, B = 0. Здесь n – число экспериментальных точек, k – число коэффициентов уравнения регрессии без свободного члена; r – коэффициент корреляции. Проверка значимости коэффициентов A и В проведена по критерию Стьюдента ( > t_кр). Гипотеза H₀: A = 0, ; гипотеза H₀: B = 0, , где s_A и s_B – стандартные отклонения коэффициентов уравнения регрессии. Доверительные интервалы: D_rG^о ± 2.303RTdlgK_LM, D_rН^о ± 2.303t_n-k-1s_BR, D_rS^о ± 2.303t_n-k-1s_AR.

Таблица 3. Параметры регрессионного анализа температурной зависимости констант устойчивости коронатов (lgK = A +B/T) и стандартные термодинамические характеристики комплексообразованияв в растворителях вода-2-PrOH

мас. доли спирта	A (sA, tнабл)	B (sB, tнабл)	r	s×10^2	lgKLK+, 298.15	DrG^0	DrH^0	TDrS^0	n; Fнабл (Fкр; tкр), DT
						кДж/моль
0	-2.37 (0.09; 26)	1310 (27; 48)	0.999	0.8	2.04 ±0.01	-11.7 ±0.06	-25 ±1.3	-13 ±1.3	7; 2265.8 (6.61; 2.57), 30
0.2	-2.18 (0.06; 37)	1379 (17; 79)	0.999	0.6	2.46 ±0.01	-14.0 ±0.06	-26 ±0.8	-12 ±0.8	8; 6257.0 (5.99; 2.45), 35
0.4	-0.83 (0.08; 10)	1087 (25; 43)	0.998	0.9	2.83 ±0.01	-16.2 ±0.06	-21 ±1.2	-5 ±1.2	8; 1859.2 (5.99; 2.45), 35
0.6	-2.93 (0.09; 32)	1794 (28; 65)	0.999	1.0	3.10 ±0.01	-17.7 ±0.06	-34 ±1.3	-16 ±1.3	8; 4261.5 (5.99; 2.45), 35
0.8	2.73 (0.04; 72)	318 (11; 28)	0.996	0.4	3.80 ±0.01	-21.7 ±0.06	-6 ±0.5	16 ±0.5	8; 771.9 (5.99; 2.45), 35
1.0	-0.19 (0.03; 7)	1251 (8; 160)	0.999	0.3	4.01 ±0.04	-22.9 ±0.06	-24 ±0.4	-1 ±0.4	8; 25230 (5.99; 2.45), 35

Литература:

1. Гаммет Л. Основы физической органической химии. М.: Мир, 1972, 512 с.

2. Бондарев Н.В. ЖФХ, 1999, 73, 74–77