Экономика/8

Броншпак Г.К.

Харьковский национальный технический университет сельского хозяйства им. П.Василенко

Об одной задаче теории игр

Обратимся к задаче из теории игр, которая рассмотрена Р.Беллманом [1, с. 307-309] и в несколько видоизмененной нами интерпретации сводится к следующему. Предполагаемая игроком вероятность, с которой он сделает правильную ставку, или же допустит ошибку, составляет соответственно и . Игрок начинает игру, располагая капиталом . Очевидно, если он должен автоматически выигрывать каждое пари. Если игрок стремиться к максимизации математического ожидания своего капитала после состязаний, то ему нужно ставить все свои деньги каждый раз, когда и не ставить ничего в случае .

Однако эта стратегия сопряжена с риском. Для любого реальная вероятность того, что на одном из шагов процесса игрок потеряет все свои деньги, очень велика. Поэтому рассмотрена более осторожная стратегия игрока, при которой он хотел бы обезопасить себя от возможного разорения. Как оказывается, для этого игрок должен руководствоваться критерием максимизации математического ожидания логарифма той суммы, которая остается у него после состязаний.

Для одношагового процесса в таком случае нужно найти максимум функции

по множеству всех из интервала . При он достигается в точке

,
где принимает значение

;
если же , то .

Для многошагового процесса такая стратегия также является оптимальной при условии, что на каждом шаге процентное отношение ставки к общей сумме, которой располагает игрок, – постоянно. Развитие этих соображений дало замечательный результат: стратегия игрока, смысл которой заключается в том, чтобы на каждом шаге ставить фиксированную долю наличного капитала, является оптимальной в классе любых политик заключения пари.

Математическое ожидание логарифма конечного капитала игрока после игр при условии, что он начал игру с капиталом и придерживался оптимальной стратегии

, (1)
где

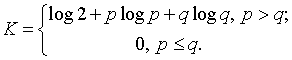
При этом оптимальная стратегия не зависит от и имеет оговоренный выше вид, а именно:

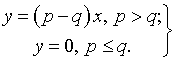(2)

Стратегия (1), несомненно, полезна для игрока, порождая весьма практичный прием (2) повышения шансов выигрыша. Но его вполне может использовать, например, розничный торговец, который систематически закупает мелкий опт приблизительно одинаковой конфигурации. Затем реализует его, получая доход, однако в условиях достаточно высокой степени рисков (подразумеваются, в частности, пропажи товара).

Поскольку статистика такого рода сделок вполне представительна и все они однотипны, торговец легко может оценить, что за истекший период, скажем, в 20% случаев он терпел убыток. Соответственно ; и для беспроигрышности своей стратегии (или же, избегания банкротства) в предстоящую сделку торговцу следует вкладывать не более, чем . Иначе говоря, 60 % имеющегося в наличии капитала. Заметим, если судить о содержании такой стратегии, пользуясь категориями здравого смысла, то она совсем не очевидна.

Представляют интерес также следующие соображения [1, с. 309-310]. Если , то принимает максимальное значение, равное . Таким образом, разница между максимумами математических ожиданий конечного капитала при и составляет

.

Для получения «стационарного» значения, это выражение следует разделить на . В результате возникает магическое число, которое играет видную роль в теории информации. Его называют также «пропускной способностью канала», используя для оценки качества систем связи. На самом деле, такой критерий должен быть связан с функцией . Из этого вытекает, что величина субъективной вероятности, которой так или иначе руководствуется игрок, делая ставку, находится в зависимости от суммы имеющихся у него средств.

Приведенные результаты представляются весьма важными для экономических приложений различной направленности. Так, они убедительно свидетельствуют об эффективности экономических кластеров. Действительно, в условиях достоверности получаемой от партнеров информации существенно снижаются риски производственно-коммерческой деятельности.

Касаясь весьма важного понятия субъективной вероятности, приведем соображения С.П.Савчука [2]. Существуют два полюса вероятности: объективная вероятность в ее частотной интерпретации и субъективная вероятность – как «разумный уровень доверия». Эта вероятность представляет количественную оценку возможности наступления события, которая задается на основании имеющегося опыта. Иначе говоря, – априорной информации о рассматриваемом процессе. Теорема Байеса с помощью элементарного преобразования позволяет получить апостериорное распределение параметра, которое является условным по отношению к первоначальной информации и эмпирическим данным. По мере накопления выборочной информации, она начинает преобладать в апостериорном распределении. Плотность его все более концентрируется вокруг истинного значения параметра. Одновременно корректируются априорные уровни доверия.

Однако, по существу, здесь подразумевается объективно присущее кластеру качество самообучения. Заметим, что в процессе обмена информаций участники кластера безвозмездно передают друг другу различного рода нематериальные активы, которые на законном основании не подлежат налогообложению. Одновременно снижаются расходы на адаптацию к рискам, а также рекламу продукции, лоббирование интересов и трансакционные издержки. В этом несомненные преимущества кластерного подхода. Теорема Байеса также очень созвучна процессу выработки решений, который характерен для метода управления по результатам [3]. Он, в свою очередь, органично сопрягается с кластерной методологией. Обратим также внимание на работу [4], в которой принятие решений трактуется с точки зрения процесса обучения и байесовского подхода.

Литература:

1. Беллман Р. Процессы регулирования с адаптацией. – М.: Наука, 1964. – 359 с.

2. Савчук В.П. Байесовские методы статистического оценивания: Надежность технических объектов. – М.: Наука, 1989. – 326 с.

3. Управление по результатам /Т.Санталайнен., Э.Воутилайнен, П.Поренне, Й.Х.Ниссинен. – М.: ИГ «ПРОГРЕСС», «УНИВЕРС», 1993. – 319 с.

4. Моррис У. Наука об управлении. Байесовский подход. – М.: Мир, 1971. – 304 с.