Ажиханов Н.Т., Батырова Л.Т.

МКТУ им.Х.А.Ясави, Казахстан, г.Туркестан

Задача фильтрации жидкости к неоднородной горизонтальной скважины в неодродной пористой среде

Исследование фильтрации жидкости через упруго-деформируемую анизотропную пористую среду необходимо для большинства месторождения, находящихся на заключительной стадии разработки. При разработке месторождении возникновения в коллекторе дополнительной емкости под действием геодинамических сил в значительной степени изменяет механизм фильтрации флюидов в пласте. При исследовании фильтрации жидкости к горизонтальным скважинам в стационарном режиме необходимо учитывать следующие факторы [1]: длительность стабилизации забойного давления и дебита; переменность забойного давления по длине горизонтального ствола при сравнительно больших дебитах скважин и длинах горизонтального ствола; ассиметричность по геологическим и технологическим причинам, расположение горизонтального ствола по толщине пласта и относительно контуров питания; отстуствие математически доказанного радиуса контура питания. С влиянием этих и многих других факторов связаны погрешности определяемых параметров скважин и пластов. Во этом разделе рассматирвается стационарный фильтрационный процесс в упругодеформируемой анизотропной (трансверсально-изотропной) пористой среде.

Рассмотрим упругое статическое состояние горизонтальной скважины, продольная ось которой составляет произвольный угол с линией простирания плоскости изотропии породного массива (рис. 1).

Пусть в расчетной области выполняется условия равновесия

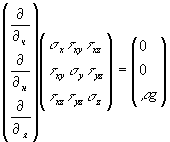(1)

где – нормальные напряжения, – касательные напряжения,

– плотность, g– ускорение свободного падения.

Введем прямоугольную декартовую систему координат Оxyz таким образом, что ось Оz направлена вертикально вверх, горизонтальные оси Оx и Оy совпадают с линиями соответственно вкрест и вдоль простирания плоскости изотропии.

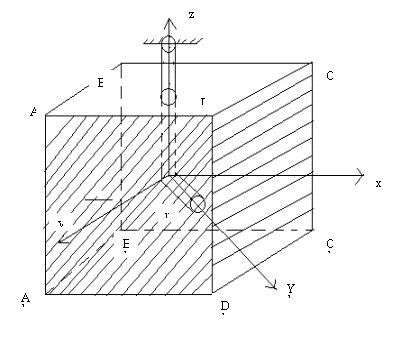
Рисунок 1. Расчетная схема горизонтальной скважины, расположенной в неоднородной пористой среде

Упругое состояние трансверсально-изотропного массива описывается уравнением обобщенного закона Гука в системе координат Ox’y’z’[1], получен-ной путем поворота Оxyz на угол вокруг вертикальной оси Oz и имеет вид

где,

Здесь коэффициенты деформации вычисляются из приведенной в работе [3] образом для массива наклонной под углом слоистых сред.

Компоненты деформации также можно определяет через перемещение , и (по оси Ox, Oy и Oz соответственно) с помощью cоотношения Коши

(2)

Граничные условие зададим в виде

, при , (3)

при

Здесь и – модули Юнга, и – коэффициенты Пуассона, – модуль сдвига, -угол наклона плоскости изотропии пласта, -угол отклонения оси Oy от линии простирания наклонной плоскости изотропии.

Далее стационарная фильтрация жидкости к горизонтальной скважине в трансверсально-изотропной пористой среде (рис.1) описывается следующим уравнением определяющий давление

(4)

с граничными условиями

(5)

где – коэффициенты проницаемости анизотропного (трансверсально-изотропного) пласта.

При этом полное напряжение трансверсально-изотропного пласта может быть выражено через эффективного напряжения и давления [2], полученные при соответствующих решениях задач (1-5) в виде

(6)

Характерной особенностью модели является предположение о том, что пористая матрица деформируется совершенно свободно до некоторого жесткого предела . Численный эксперимент проводился по следующим данным: в качестве пород наклонных слоем взяты [3]. Аргилит, Алевролит, Песчаник, Известяк модуль упругости которых имеет соответственно значения постоянная Пуассона соответственно . Для трансверсально-изотропных слоев округленные упругие характеристики определяется

Модуль сдвига ; , .

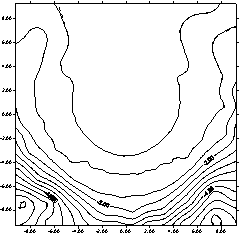
При этом граничные условия (2) учитывается при определений напряжение наклонном под пласте по и . Сравнительные изолиний показаны рис.2 в в случаях (пунктирные линии) и (сплошные линий). Общий вид функции деформации представлены в рис.3.

а)

б)

Рис.2. Изолинии нормальных напряжений а) б)

Анализ результатов, приведенных в наклонном трансверсально-изоторпном пласте, показывает, что с увеличением количества конечных элементов в дискретной модели тела, наблюдается совпадение двух значащих цифр в значениях компоненты перемещения u, нормальных напряжения σ_, а также в значениях интерсивности напряжений и деформаций. Таким образом, можно получит оценку влияния давления жидкости в напряженно-деформируемое состояние неоднородного пласта.

ЛИТЕРАТУРА

1. Мехницкий С.Г. Теория упругости анизотропного тела. М., Наука. 416 с.

2. Фадеев А.Б. Метод конечных эелементов в геомеханике. М., Недра, 1987

3. Масанов Ж.К., Ержанов Ж.С., Айталиев Ш.М. Устойчивость горизонталь-ных выработок в наклонно-слоистом массиве. Алма-Ата, Наука, 1971,160с.