Дронсейка И.П., Тыныбекова С.Д.

Восточно-Казахстанский государственный технический университет

им. Д. Серикбаева, Казахстан

ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ – НЕОТЪЕМЛЕМАЯ ЧАСТЬ ПЕДАГОГИЧЕСКОГО ПРОЦЕССА

Одной из актуальных тенденций развития современного высшего образования является его информатизация. Внедрение информационных технологий – это не только один из наиболее эффективных методов достижения педагогических задач, но и неотъемлемая часть современного образовательного процесса. Среди важнейших задач, стоящих сегодня перед любым преподавателем высшей школы, можно выделить следующие: повышение уровня учебной мотивации студентов и формирование способности к самообразованию.

В современном образовании применение информационно-коммута-ционных технологий (ИКТ) на различных занятиях (лекции, практические занятия, занятия по СРСП и т.д.) становится распространенным явлением. Правильное использование в учебном процессе компьютера, который является техническим средством обучения, позволяет осуществлять учебный процесс в новых условиях, когда педагог перестает для обучающихся быть единственным источником информации.

В этом преподавателю помогает новое современное техническое средство обучения – интерактивная доска, которая пришла на смену меловой и даже маркерной доске. Это оборудование, которое способно оказать неоценимую помощь преподавателю в организации процесса обучения.

Интерактивная доска –устройство, внешним видом и размерами очень похожее на обычную доску, – это сенсорный экран, подсоединенный к компьютеру, изображение с которого передает на доску проектор. С помощью проектора изображение рабочего стола компьютера проецируется на поверхность интерактивной доски. В этом случае доска выступает как экран. С проецируемым на доску изображением можно работать, вносить изменения и пометки. Все изменения записываются в соответствующие файлы на компьютере, могут быть сохранены и в дальнейшем отредактированы или переписаны на съемные носители.

Интерактивная доска работает вместе с компьютером и видеопроектором, представляя собой единый комплекс. На ней можно делать все то же, что и на обычном компьютере, при этом связь доски и компьютера двусторонняя. Другими словами, интерактивная доска работает как сенсорный компьютерный монитор. В интерактивной доске объеденены проекционные технологии с сенсорным устройством, поэтому такая доска не просто отображает то, что происходит на компьютере, а именно:

· позволяет управлять процессом презентации,

· вносить поправки и коррективы, делать цветом пометки и комментарии,

· сохранять материалы занятия для дальнейшего использования и редактирования.

В результате учебное время занятия организуется более рационально, расширяются возможности в выборе средств и методов обучения, повышается мотивация обучающихся и их активность на занятиях. Успешность обучения во многом зависит от форм организации познавательной деятельности обучающихся, взаимодействия преподавателя и студентов.

Безусловно, использование интерактивной доски не решит всех проблем, возникающих в процессе обучения. Современному преподавателю необходимо уметь активно использовать имеющийся на вооружении технический арсенал, в частности интерактивную доску, для эффективной организации учебного процесса. И здесь у каждого преподавателя свои практические приемы и тонкости. Остановимся на некоторых моментах из личного опыта организации занятий с использованием интерактивной доски StarВoard компании Hitachi.

Одной из особенностей программного обеспечения интерактивных досок является возможность работы в двух режимах: обычном (постраничном), и полноэкранном. Обычный режим обеспечивает «сквозное» просматривание всего материала, облегчает его выбор в течение занятия. Полноэкранный режим удобен для фронтальной работы, так как весь материал страницы хорошо просматривается с любого места в аудитории.

Использование интерактивной доски способствует повышению эффективности одной из распространенных форм деятельности обучающихся на занятии – фронтальной работе, поскольку позволяет создать условия для повышения активности студентов. Достигается это возможностью включения обучающихся в непосредственную работу с предлагаемым материалом: просмотр и прослушивание материала, выделение, создание и перемещение информационных объектов и другие действия, что позволяет проводить интерактивные занятия с целью завладеть вниманием студентов, углубить их понимание преподаваемой дисциплины.

В качестве примера приведем задание по дисциплине «Дифференциальные уравнения» для студентов второго курса специальности «Математическое и компьютерное моделирование» [5В070500] по теме «Линейные дифферен-циальные уравнения первого порядка». Студентам были предложены два различных метода решения данных уравнений: метод вариации произвольных постоянных и метод Бернулли, описанные ниже.

Дифференциальное уравнение, содержащее искомую функцию и ее производную только в первой степени, называется линейным.

Линейные уравнения первого порядка имеют вид:

, (1)

, (2)

где и – непрерывные функции, и называются соответственно (1) – неоднородным, (2) – однородным.

Найдем общее решение однородного уравнения

. (3)

Методом Лагранжа (методом вариации произвольной постоянной) найдем решение уравнения (1). Решение ищем в виде (3), где – неизвестная функция. Подставляя вместо выражение

,

а вместо – (3), получим

.

Подставляя в (3), получим общее решение уравнения (1)

. (4)

Пример 1. Найти общее решение уравнения ; решить задачу Коши при начальном условии .

Решение. Приведем данное уравнение к виду (3), разделив обе его части на :

Здесь ,

Общее решение исходного уравнения в соответствии с формулой (4) имеет вид

(5)

Найдем входящие в это выражение интегралы. Имеем

где знаки и появляются в силу равенства Подставляя найденные интегралы в решение (5), получаем общее решение уравнения:

.

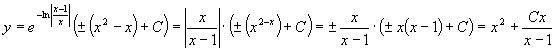Отсюда выделяем частное решение, соответствующее начальному условию:

Отметим, что линейное дифференциальное уравнение (1) можно также проинтегрировать методом Бернулли, суть которого заключается в следующем.

Общее решение линейного уравнения (1) ищем в виде , где и – неизвестные функции от (одна из этих функций может быть выбрана произвольно). Так как , то, подставляя выражения и в уравнение (1), получим

или

. (6)

Подберем функцию так, чтобы выражение, стоящее в скобках, обратилось в нуль, т.е.

.

Решая это уравнение, найдем :

, Þ , Þ

Интегрируя, получим .

Так как функция может быть выбрана произвольно, можно принять . Тогда . Подставляя найденную функцию в уравнение (6), получим .

Решая это уравнение, найдем :

, Þ _Þ .

Тогда общее решение данного линейного уравнения (1) будет иметь вид

.

Пример 2. Решить задачу Коши , .

Решение. Данное уравнение линейное, сначала найдем общее решение.

Положим , . Подставим и в уравнение

,

. (*)

Так как есть произведение двух функций и , то одна из них может быть выбрана произвольно. Положим или . Проинтегрировав, получим частное решение : , Þ .

При равенство (*) обратится в уравнение , Þ .

Откуда , и общим решением данного уравнения будет

.

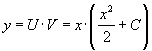Теперь найдем значение постоянной , при котором частное решение удовлетворяет начальному условию . Следовательно, и частное решение принимает вид .

На одной странице показан один метод, на другой – второй (обе страницы одновременно представлены на интерактивной доске) и дано задание – сравнить два метода, результатом которых является одна и та же формула общего решения уравнения указанного вида, разобрать примеры.

Таким образом, использование интерактивной доски позволяет обучающимся увидеть, сравнить и сохранить различные варианты решения. Такой метод способствует улучшению познавательной деятельности студентов, позволяет значительно повысить качество преподавания за счет сочетания традиционных и компьютерных методов организации учебной деятельности.

Литература:

1. Горюнова М.А., Семенова Т.В., Солоневичева М.Н. Интерактивные доски и их использование в учебном процессе. – СПб: БХВ-Петербург, 2010.

2. Свободная энциклопедия Википедия. – http://ru.wikipedia.org/