Экономическин науки/ 8. Математические методы в экономике
К.э.н. Андриенко В.М., магистр Голованова
Е.Ю.
Одесский национальный
политехнический університет
ВЫЧИСЛЕНИЕ БИРЖЕВЫХ ЦЕН МЕТОДОМ
СЛУЧАЙНЫХ БЛУЖДАНИЙ
Рынок ценных бумаг, являясь одной из составляющих
рыночной экономики, имеет возможности через свои механизмы мобилизовать
инвестиционные ресурсы в целях экономического роста, развития научно-технического
прогресса, инновационной деятельности, освоения нових производств.
Все операции с ценными
бумагами всегда сопряжены с риском. В этой связи построение математических
моделей, позволяющих лучше понять структуру и поведение рынка как единого
целого, так и его составляющих, долгое время привлекали и продолжают привлекать
внимание исследователей и практиков. Эти модели важны и для инвесторов,
интересующихся возможностью прогнозирования поведения цен финансовых активов, и
для регулирующих органов, которых интересует возможность влияния на рынок так,
чтобы он наилучшим образом соответствовал целям развития экономики. Попытки построить модели цен и доходностей ценных
бумаг предпринимались еще с начала ХХ в. Французский ученый Л.Башелье,
опубликовавший свою работу в начале 1900-х годов , предложил нормальную модель
для цен финансовых активов и товаров, которые основаны на центральной предельной теореме. В течение ХХ в.
предложение о нормальности цен и доходностей использовалось во многих моделях,
в частности, в моделе выбора портфеля Марковица-Шарпа и в методике RickMetrics. В 1964 году В.Шарп предложил модель CAPM (Capital Asset Pricing Model), а в 1976
году С.Росс представил теорию APT
(Arbitrage Pricing Theory). Обе эти теории, ставшие в последствии
классическими, составляют ядро современной теории финансов. Практика показала,
что гипотеза о нормальности цен и доходностей приемлема только на очень
небольших интервалах времени. При увеличении интервалов она обычно плохо
соответствует данным. Лучше соответствует данным так называемая логнормальная
модель. Логнормальное распределение с параметрами ![]() характеризуется функцией распределения
характеризуется функцией распределения
![]() (1)
(1)
Математическое ожидание и дисперсия
вычисляются соответственно по формулам (2) и (3)
![]() (2)
(2)
![]() (3)
(3)
Кривые плотности логнормального и нормального распределений изображены соответственно на Рисунках 1 и 2.

Рисунок
1. Плотность логнормального
Рисунок 2. Плотность нормального
распределения. распределения.
Затем ученые пришли к выводу, что лучше рассматривать не изменения цен, а приращения их логарифмов. Так возникла
концепция геометрического (экономического) броуновского движения П.Самуэльсона. Процесс геометрического
броуновского движения отражает уравнение (4), а графически Рисунок 3.
 (4)
(4)
где ![]() - цена некоторого
рискового (со случайной доходностью) актива на момент
- цена некоторого
рискового (со случайной доходностью) актива на момент ![]() , при этом предполагается, что актив бездивидентный, то есть,
весь его доход состоит только в
повышении цены актива,
, при этом предполагается, что актив бездивидентный, то есть,
весь его доход состоит только в
повышении цены актива, ![]() - цена актива в момент времени t=0,
- цена актива в момент времени t=0, ![]() - годовая ставка
доходности актива,
- годовая ставка
доходности актива, ![]() - годовая волатильность ,
- годовая волатильность , ![]() - нормально распределенная случайная величина с
нулевым математическим ожиданием и дисперсией
- нормально распределенная случайная величина с
нулевым математическим ожиданием и дисперсией ![]() .
.
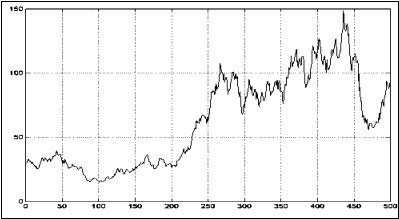

Рисунок 3. Процесс геометрического броуновского
движения
Вместо начального момента ![]() можно взять
произвольное
можно взять
произвольное ![]() , тогда в качестве начальной цены вместо
, тогда в качестве начальной цены вместо ![]() нужно взять
нужно взять ![]() . Цена актива
. Цена актива ![]() имеет логнормальное
распределение. Пользуясь формулами (2,3) выпишем выражения
для математического ожидания и дисперсии:
имеет логнормальное
распределение. Пользуясь формулами (2,3) выпишем выражения
для математического ожидания и дисперсии:
![]() ,
, ![]() (5)
(5)
Вскоре модель Самуэльсона подверглась критике. Дело в
том, что на больших объемах эмпирических данных модель не согласуется с фактическими данными. Появились уточнения
модели геометрического броуновского движения, например, ARCH, GARCH и др. Затем
стали рассматривать волатильность ![]() переменной величиной
во времени. Однако, эти уточнения либо
малоэффективны, либо приводят к сложным математическим алгоритмам. На сегодняшний день большое распространение среди
профессиональных инвесторов получили пакеты, основанные на нейросетевых методах
и фрактальной теории. Такие пакеты обладают некоторыми способностями адаптироваться
к рынку. Проблема заключается в том, что законы рынка меняются, а модели, встроенные
в пакеты, остаются прежними. В результате, пакет со временем утрачивает
способность к адаптации, а финансовый менеджер, не имея возможности
перепрограммировать готовый пакет, принимает решения на основе устаревших
моделей.
переменной величиной
во времени. Однако, эти уточнения либо
малоэффективны, либо приводят к сложным математическим алгоритмам. На сегодняшний день большое распространение среди
профессиональных инвесторов получили пакеты, основанные на нейросетевых методах
и фрактальной теории. Такие пакеты обладают некоторыми способностями адаптироваться
к рынку. Проблема заключается в том, что законы рынка меняются, а модели, встроенные
в пакеты, остаются прежними. В результате, пакет со временем утрачивает
способность к адаптации, а финансовый менеджер, не имея возможности
перепрограммировать готовый пакет, принимает решения на основе устаревших
моделей.
Модель геометрического броуновского
движения является достаточно простой и легко реализуется на практике, поэтому
она является привлекательной для менеджеров. Однако, переменными во времени следует считать оба параметра модели.
Рассмотрим практический подход в реализации этой идеи. В формулах (5) выразим ![]() и
и ![]() :
:
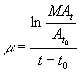 (6)
(6)
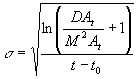 (7)
(7)
В качестве ![]() и
и ![]() возьмем оценки этих
характеристик по эмпирическим данным,
полученным методом подстановки :
возьмем оценки этих
характеристик по эмпирическим данным,
полученным методом подстановки :
![]() =
=![]() (8)
(8)
![]() =
=![]() , (9)
, (9)
где ![]() - значения
эмпирического ряда,
- значения
эмпирического ряда, ![]() - число значений эмпирического ряда.
- число значений эмпирического ряда.
Таким образом, по мере поступления новых эмпирических
данных, можно производить коррекцию геометрического
броуновского процесса (4) в реальной ситуации. Для правильного расчета по
формуле (4) необходимо задать масштаб времени. Если используются годовые
показатели волатильности и доходности, то временной масштаб, соответствующий
году, принимается равным единице, а один день составляет 1/k (k –число
торговых дней в рассматриваемом году).
На
рисунке 7 приведены графики фактических (жирным) и прогнозных цен паев ПИФов
компании «Укртелеком» на 2007 год при постоянных ![]() и
и ![]() , вычисленных на основе данных за 215 торговых дней 2006
года (здесь и в дальнейшем приведены данные сайта www.uapif.com). На оси абсцисс показаны номера периодов. Временной
период в данном случае равен одному дню и составляет
, вычисленных на основе данных за 215 торговых дней 2006
года (здесь и в дальнейшем приведены данные сайта www.uapif.com). На оси абсцисс показаны номера периодов. Временной
период в данном случае равен одному дню и составляет ![]() . Среднегодовая волатильность при этом равна
. Среднегодовая волатильность при этом равна ![]() = 0,007, а среднегодовая доходность
= 0,007, а среднегодовая доходность ![]() = 0,34, величины
= 0,34, величины ![]() вычислены с помощью
генератора случайных чисел пакета «Анализ данных» в Microsoft Ecxel.
вычислены с помощью
генератора случайных чисел пакета «Анализ данных» в Microsoft Ecxel.

Рисунок 7. Динамика фактических и прогнозных данных на
2007 г. цен паев ПИФов компании «Укртелеком»
Из рисунка видно, что только на двух участках, c 38
по 40 день и с 60 по 120 день прогнозные данные согласуются с фактическими, а
на остальных – существенно расходятся.
На Рисунке 8 приведены графики фактических
(жирным) и прогнозных цен паев ПИФов компании «Укртелеком» на
2007 год при переменных ![]() и
и ![]() . Параметры пересчитывались по мере появления данных за 2007
год каждые 30 дней, при этом момент времени
. Параметры пересчитывались по мере появления данных за 2007
год каждые 30 дней, при этом момент времени ![]() сдвигался на 30 дней,
таким образом число временных периодов оставалось постоянным, равным 215. Однако,
корректировка формулы (4) производилась дважды, в точках, соответствующих 120 и
150 временным периодам (120 и 150 дням 2007 года). До этого момента времени
параметры
сдвигался на 30 дней,
таким образом число временных периодов оставалось постоянным, равным 215. Однако,
корректировка формулы (4) производилась дважды, в точках, соответствующих 120 и
150 временным периодам (120 и 150 дням 2007 года). До этого момента времени
параметры ![]() и
и ![]() оставались
практически неизменными, а после этого
момента, до конца прогнозного периода оставалось немного точек, и необходимость
корректировки на этом интервале утратила свою актуальность. На приведенном рисунке 8 прогнозные точки
получены при следующих значениях параметров:
оставались
практически неизменными, а после этого
момента, до конца прогнозного периода оставалось немного точек, и необходимость
корректировки на этом интервале утратила свою актуальность. На приведенном рисунке 8 прогнозные точки
получены при следующих значениях параметров: ![]() =0,074 и
=0,074 и ![]() =0,007. Критерием качества прогноза рассматривалась сумма
квадратов отклонений прогнозных значений от фактических. В первом случае
значение критерия равно 3,8855 во втором -
0,4187. Таким образом, корректировка параметров геометрического
броуновского движения на порядок улучшила прогноз.
=0,007. Критерием качества прогноза рассматривалась сумма
квадратов отклонений прогнозных значений от фактических. В первом случае
значение критерия равно 3,8855 во втором -
0,4187. Таким образом, корректировка параметров геометрического
броуновского движения на порядок улучшила прогноз.

Рисунок 8. Динамика фактических и откорректированных
прогнозных данных на 2007 г. цен паев ПИФов компании «Укртелеком»
В приведенном примере на процесс в большей степени
влияет параметр доходности ![]() , а параметр волатильности
, а параметр волатильности ![]() практически оставался
неизменным, в пределах 0,006-0,007. Практика показала, что корректировку
процесса (4) следует производить в середине текущего периода. В точках,
расположенных вблизи границы откорректированный результат может оказаться
хуже предыдущего. Чаще, чем через 30-50 дней корректировку производить не
следует, параметры меняются достаточно медленно. Примененная вычислительная
процедура легко реализуется в Microsoft Excel.
практически оставался
неизменным, в пределах 0,006-0,007. Практика показала, что корректировку
процесса (4) следует производить в середине текущего периода. В точках,
расположенных вблизи границы откорректированный результат может оказаться
хуже предыдущего. Чаще, чем через 30-50 дней корректировку производить не
следует, параметры меняются достаточно медленно. Примененная вычислительная
процедура легко реализуется в Microsoft Excel.
Литература:
1.
А.Г.Шоломицкий,. Теория риска- М.:Издательский
дом ГУ ВШЭ, 2005- 395 с.
2.
В.Ю. Королев, В.Е.
Бенинг, С.Я. Шоргин. Математические основы теории риска- М.:ФИЗМАТЛИТ, 2007-380.
3.
В. Феллер. Введение в
теорию вероятностей и ее приложения, Т.2.-М.:Мир 1984-761с.