Лукашенко А.Г., Лукашенко Д.А., Дахно С.В.,

Караван М.А., Уткіна Т.Ю, Чичужко М.В.

Черкаський державний технологічний університет, Україна

Високонадійна модель керування траєкторіями руху виконавчих механізмів

В технологічних процесах при паралельній координації дій виконавчих механізмів необхідно контролювати моменти часу, в які механізми досягають певного положення по заданим траєкторіям. Звичайно в підсистемах управління використовуються цифрові таблиці значення функцій, як еталон для порівняння з поточним значенням координат.

Складність завдань, що вирішуються цифровими обчислювальними машинами постійно росте, підвищення вимог до точності, часу і достовірності результатів рішення, простоти програмування і зручності обслуговування, а також обмеження, що часто накладаються, на габаритні розміри, вага і вартість обчислювальних машин тісним чином пов'язані з проблемою підвищення ефективності роботи сучасних спеціалізованих комп’ютерних систем. Досягнення максимальної ефективності, за словами академіка В. М. Глушкова, в значній мірі визначається оптимальним співвідношенням програмних і апаратурних засобів системи математичного забезпечення (МЗ). Безперервне вдосконалення технології виробництва електронних схем привело останнім часом до різкої диспропорції між вартістю програмних (software) і апаратурних (hardware) засобів системи МЗ. Якщо вартість електронних компонентів постійно зменшується, то витрати на програмну частину неухильно зростають. Апаратурна реалізація засобів МЗ в порівнянні з програмною має також ряд переваг в плані швидкодії, надійності і простоти програмування [1].

Інтерес представляє метод апаратурної реалізації для відтворення функцій описаних в роботах [2, 3, 4], що здійснюється у вигляді суперпозиції трансформованої по цілим степеням двійки кодової послідовності аргументу і коректуючої константи.

При цьому для ділянки зміни аргументу функція подається в такому вигляді:

(1)

де x – аргумент функції;

q – основа прийнятої системи лічення;

m – розрядність коефіцієнту нахилу апроксимуючої прямої;

ξ_(0j)…ξ_(m-1)j – константи перетворення, що мають значення 0 або 1;

Δ_j – значення коректуючих констант, визначених як сума по mod 2 значення трансформованої кодової послідовності вхідного аргументу і відповідного йому значення кодової послідовності функції.

Кількість і знаки зміщень вибираються із врахуванням необхідної точності відтворення функції. Процедура розрахунку функцій, що реалізується, зумовлюється тим, що визначається значення коректуючої константи й коефіцієнта нахилу прямої на j-ій лінійній ділянці апроксимації.

Відомий пристрій [4], який реалізує функцію (1) має недолік – мала надійність із-за великої кількості зовнішніх контактних вузлів.

Основними причинами відмови пристроїв у процесі зборки кристалів в корпус та установці на друковану плату є недостатня механічна міцність контактів, мала адгезія виводів до контактної площадки і останньої до підложи, деградації контактного опору через взаємну дифузію металів з утворенням інтерметалевих фаз і пустот, або прихованого технологічного дефекту.

Під контактним вузлом приймається система: струмоведуча площина металізації – термокомпресія – провідник – контактний вивід корпусу – міжз’єднання до струмоведучої площадки друкованої плати.

Пропонується високонадійна образно-знакова модель формування тригонометричних функцій, що представлена на рис. 2.

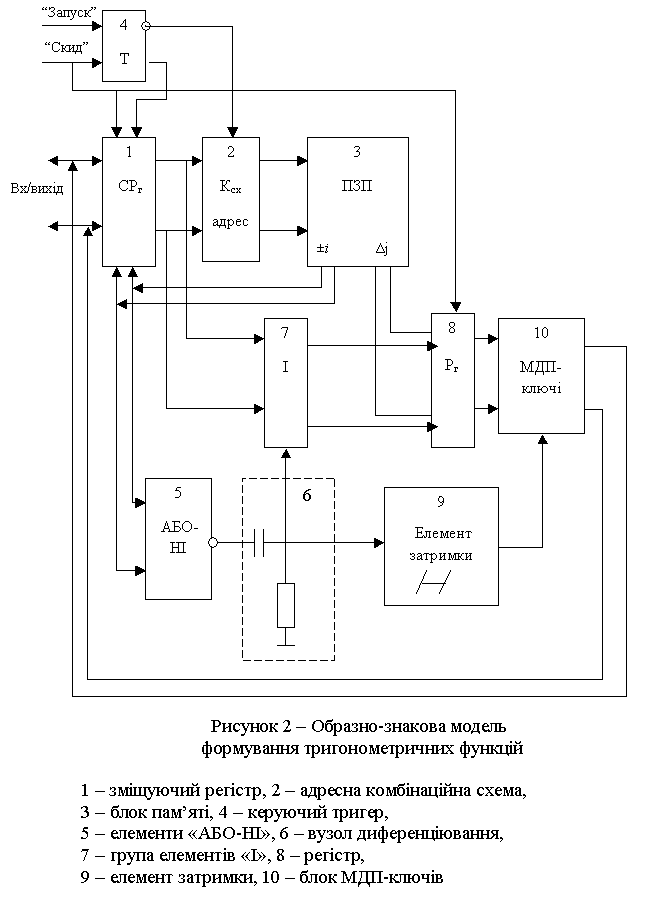
Із рис.2 видно, що підвищення надійності здійснюється шляхом схемотехнічного вирішення, у вигляді введення кодових шин "вхід/вихід".

Припустимо, інтенсивність відмов кожного контактного вузла при операціях, дорівнює : термокомпресія провідника до металізованої площадки - l₁=10^-6; термокомпресія провідника до контакту площини корпусу - l₂= 10^-6; контакт виводів корпусу ІС до друкованої плати - l₃= 10^-6.

Тоді загальна інтенсивність відмови одного контактного вузла дорівнює

l_з = l₁+l₂+l₃= 10^-6 +10^-6 +10^-6= 3×10^-6.

Наприклад, у пристроїв при обробці інформаційних операндів з розрядністю 32 загальна інтенсивність відмов контактних вузлів дорівнює

32×l_з= 32×3×10^-6= 96×10^-6.

Тоді середній час безвідмовної роботи T_р пристроїв дорівнює

T_р= (1/ål_і).

Припустимо, що для пристроїв з числом контактних вузлів 32 інтенсивність відмови пристрою без об’єднаних входів та виходів дорівнює

l_{з пр}= 96×10^-6, а у запропонованого пристрою з новою схемотехнікою – зменшується число контактних вузлів в 2 рази, тоді l_{з вин}= (96/2)·10^-6 тобто за рахунок зменшення кількості контактних вузлів інтенсивність відмови у запропонованої образно-знакової моделі формування тригонометричних функцій зменшується в 2 рази.

Це забезпечує збільшення середнього часу безвідмовної роботи моделі формування тригонометричних функцій, відповідно [2] в

Т_{р вин} / Т_{р пр} = (1/ål_і) _вин /(1/ål_і)_пр рази

де Т_{р пр} - середній час безвідмовної роботи пристрою без об’єднаних входів та виходів;

Т_{р вин} - середній час безвідмовної роботи запропонованого пристрою з новою схемотехнічною реалізацією.

Тоді для наведеного прикладу середній час безвідмовної роботи збільшується в

Т_из/Т_пр = 96·10^-6/(96/2)·10^-6 = 2 рази

Отже, зменшення кількості контактних вузлів (припустимо) в 2 рази при збереженні паралельної обробки операндів високої точності зменшує середній час безвідмовної роботи в 2 рази.

Надійність пристроїв для формування тригонометричних функцій, які створюються у вигляді інтегральних мікросхем підвищується за рахунок того, що інтенсивність відмов l контактних вузлів всередині схеми на три, …, чотири порядки менша в порівнянні з формуванням зовнішніх контактних вузлів. Цифровий пристрій, який реалізовано в єдиному кристалі, завдяки зменшенню кількості зовнішніх контактів буде більш відмовостійким і тому підвищує не тільки надійність пристрою,а й відсоток виходу придатних ІС, що знижує вартість цифрового пристрою для обчислення функцій [2].

Література

1. Балашов Е.П., Смолов В.Б., Смагин А.А., Кокаев О.Г., Уланов В.И. К вопросу применения сокращенных таблиц для построения высокопроизводительных однородных процессоров // Управляющие системы и машины. – 1975. - №3. - С. 99-102.

2. Лукашенко В.М. Быстродействующие высоконадежные функционально ориентированные преобразователи // Сучасні інформаційні та енергозберігаючі технології життєзабезпечення людини. – К. ФАДА, ЛТД. -1999. №6. – С. 386-392.

3. Лукашенко В.М. Таблично-алгоритмічні методи, моделі формування та перетворення функціонально орієнтованих процесів для апаратурної реалізації // Монографія. Черкасский государственный технологический университет. – Черкаси: 2002. – 165 с. - Укр. – Деп. в НИИТЭХИМ г. Черкассы 20.06.2002. № II–xn 2002. // Анот. Библ. Указ.ВИНИТИ “Деп. научные работы” - №9. – 2002.

4. Пат. 30645 А Україна, МПК G 06 G 07/26; Цифровий пристрій для обчислення функцій. В.М. Лукашенко ЧІТІ UA. - № 98041690; Заявл. 02.04.1998; Опубл. 15.12.2000; Бюл. - №7. – 3 с.