В.Г. Красиленко, к.т.н., с.н.с., доц..,

                                                         Л.І. Іванова, ст. викл.,

                                                         О.В. Краснокутський, студент

                                                                                ВСЕі Університету «Україна», м.Вінниця

 

 

 

 

 

 

Проектування та дослідження базових вузлів векторних процесорів з часоімпульсним кодуванням

 

Вступ. Мережа нейронів, яка утворює людський мозок, являє собою комплексну високоефективну, суттєво-паралельну систему обробки інформації, що таким чином організовує своє функціонування, щоб реалізувати сприйняття образів та їх розпізнавання набагато швидше та ефективніше, ніж найсучасніші комп’ютери традиційної архітектури. Нейрофізіологами встановлено, що: мозок має комірчасту структуру, нейрони передають інформацію у вигляді коротких електричних імпульсів, швидкість їх розповсюдження обмежена (приблизно 100 м/с), а імпульси з урахуванням затухання необхідно регенерувати, що кожен нейрон інтегрує сигнали для активізації виходу більше ніж з 1000 синаптичних входів, включно важлива роль синапів в навчанні, мозок дорослої людини відрізняється від мозку новонародженої дитини лише впорядкованістю міжнейронних зв’язків. Без сумніву і те, що мозок працює не лише більш ефективно, але й принципово іншим чином, ніж звичайна ЕОМ з традиційною архітектурою. Тому, саме ці факти спричиняють та направляють роботу вчених на створення та дослідження штучних нейронних мереж (ШНМ), як паралельних розподілених багатопроцесорних систем, яким властива здатність до збереження та використання досвіду і знань, які отримуються в процесі навчання та зберігаються у вигляді сили міжнейронних синаптичних зв’язків.

Огляд публікацій. Значним результатом, на наш погляд, в створенні ШНМ є розробка «еквівалентнісних» моделей ШНМ та розробка відповідної «еквівалентнісної» парадигми  [1, 2], які дозволяють описувати процеси функціонування, алгоритми навчання, розпізнавання, пояснюють динаміку процесів в ШНМ, обґрунтовують перспективні апаратні реалізації. Комп’ютерне моделювання «еквіватентнісних» нейромережних моделей (ЕНММ) продемонструвало їх ефективність та суттєві переваги: збільшення ємності до ; де N – кількість нейронів та можливість просторово-інваріантного розпізнання сильнокорельованих 2.D- та 1.D- образів [3, 4, 5]. Але теоретичний фундамент нової «еквівалентнісної» парадигми потребує і нового апаратного інструментарію з високопродуктивною паралельною адаптивною обробкою та запозиченими у природи принципами і механізмами. При створенні технічних моделей нейронів кінцевою метою є розробка функціональних елементів з властивостями реальних нейронів. Але при цьому немає потреби відтворювати всі відомі властивості – важливо відобразити лише особливості, що відносяться до процесів передачі і обробки інформації. Значним фундаментом для розробки відповідного апаратного інструментарію та побудови новітнього макроелементного базису стало розширення скалярної нейробіологіки (НБЛ) і створення математичного апарату матричної нейробіологіки з її базовими операціями нормованих еквівалентностей (нееквівалентностей) двох векторів, «еквівалентнісних» просторових функцій 2D- образів, операціями автоеквівалентнісних нелінійних перетворень [4, 5] та цілим сімейством нових «еквівалентнісних» операцій на основі використання узагальнюючих операцій безперервної нечіткої та нейронечіткої логіки: нечіткого заперечення, t-норми, s-норми [6].

Розроблено десятки різних математичних та фізичних моделей нейронів, але більшість з них реалізують старі моделі, а ті, що відповідають «еквівалентнісній» парадигмі мають ряд недоліків: обмежені функціональні можливості, складність. На роль центральної проблеми при створенні базових вузлів нетрадиційних високопродуктивних процесорів та нейронних модулів ШНМ ми висуваємо проблему логічної універсалізації та інтелектуалізації (розширення набору виконуваних функцій, але до їх квазіуніверсальності при найбільш узагальнюючих матричних аналогових нейрологіках). Такі вузли та нейрони повинні мати швидку програмовану переднастройку на вид функціонального, логічного перетворення, на вид та параметри вхідного та вихідного операторів, потрібну точність обробки та запам’ятовування.

Аналіз математичних моделей нейронів, відомих правил навчання ШНМ, законів адаптації вагових коефіцієнтів міжз’єднань; математичного апарату, що використовується в системах розпізнавання, прогнозування, нейронечітких класифікаторах, експертних та діагностичних системах, показує, що є нагальна потреба в апаратній реалізації векторних, векторно-матричних, матрично-матричних та матрично-тензорних процедур з використанням більш загальних алгебр (матричних, векторних) та логік (нейронної, неперервної, гібридної, нечіткої, тощо).

Постановка задачі. Тому метою нашої роботи є представлення результатів проектування та дослідження векторних процесорів, в тому числі скалярно-реляторних, з часоімпульсним кодуванням. Вхідними операндами векторних процесорів є вектори, елементи яких є нормовані аналогові змінні   є [0, 1]. Скалярно-реляторні векторні процесори (СРВП)названі нами так, тому що вони обробляючи два и більше векторів, можуть обчислювати не лише скалярні добутки векторів, а й інші другі міри (відношення порядку) та другі оператори від вхідних векторних аргументів. Одним з перспективних напрямків при створенні таких процесорів є використання структур та їх базових вузлів з часоімпульсним кодуванням, яке було обґрунтоване та розглянуте і розвинене в роботах [7, 8]. Використання часоімпульсного кодування (ЧІК) неперервнологічних змінних дворівневими оптичними (електричними) сигналами не тільки збільшує завадостійкість, стабільність та спрощення і повторюваність при цифровій реалізації, але і суттєво розширює функціональні можливості при одночасному спрощенні принципів настроювання, управління та переднавчання.

Результати. Виходячи з архітектурних побудов та вибраного ЧІК-кодування ми визначимо в доповіді вимоги до СРВП і покажемо, що лінійні (1-D масиви) таких СРВП реалізують необхідні векторно-матричні обчислювальні процедури з лінійною та нелінійною обробкою компонентів, а 2-D масиви – реалізують матрично-матричні процедури за  часових цикла. Потім нами будуть показані результати моделювання значного набору операцій нейробіологіки, що виконуються СРВП, в тому числі результати обробки ними зображень. Структурна схема СРВП показана на рис. 1.

Компоненти (неперервнологічні змінні:  ) вхідних векторів (операндів) (в найпростішому випадку К=2, тобто лише двох векторів та ) поступають на відповідні -ті квазіуніверсальні логічні елементи неперервної (нейронної) логіки (КУЛЕі НЛ), на виході яких формуються вихідні функції  НЛ, кожна з яких є однією з можливого набору функцій-відображень  у відповідній алгебрі НЛ. Вибір функцій здійснюється векторами .

 

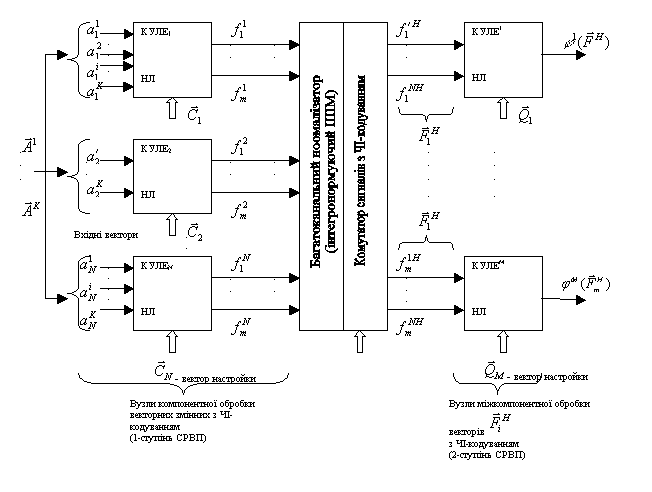
Рис.1 Структура СРВП

В найпростіших випадках  або . Оскільки при ЧІК з періодом обробки Т, функція  в часовому представленні в деяких ситуаціях може мати розриви.

 

Використання багатоканального інтегронормуючого широтноімпульсного модулятора (ШІМ) дозволяє синхронізувати (зробити стартстопну прив’язку) всі часові операнди. Останні через комутатор поступають на відповідні КУЛЕm НЛ 2го ступеня СРВП, які реалізують міжкомпонентну обробку, тобто обчислюють неперервнологічну функцію  від аргументів НЛ, що є НЛ-змінними компонентами відповідного вектора .

Таким чином одним з базових вузлів СРВП є КУЛЕ НЛ. Нормалізатори та ШІМ з часовим та просторовочасовим нелінійним інтегруванням описані в [9], а варіанти деяких реалізацій КУЛЕ НЛ з ЧІК описані в [10] і реалізовані як універсальні логічні елементи двозначної логіки (УЛЕ ДЛ) на віддзеркалювачах струму (ВС). Результати проектування та моделювання таких УЛЕ ДЛ на ВС за допомогою програм PSpise та Orcad-15, розглянуті в [10], показують, що ВС на базі  технології КМОП-транзисторів дозволяють досягати часу обробки , рівня ЧІК – операндів з амплітудами струму  та потужності енергоспоживання на рівні , крім того, відносні похибки при реалізації функцій еквівалентності (нееквівалентності), як окремого випадку , можуть не перевищувати .

Нами запропоновано також підхід, при якому можна синтезувати схему КУЛЕ НЛ, використовуючи схожість деяких структурних фрагментів в схемах різних не універсальних ЛЕ НЛ, їх композицію та просту структурну настройку на усю можливу множину функцій НЛ. Ще один підхід полягає у використанні для реалізації КУЛЕ НЛ на базі універсальних елементів порядкової логіки.

Висновки. Проектування СРВП потребує синтезу їх базових вузлів – КУЛЕ НЛ, а останні можна реалізувати на основі УЛЕ ДЛ при використанні часоімпульсного кодування.

Література

1.        Красиленко В.Г. та інші. Демонстрація ефективності еквівалентнісних моделей нейронних мереж з адаптивно-кореляційними коригуваннями матриці зв’язків. ВОТТП, №4, 2000.

2.        Красиленко В.Г. та інші. Деякі новітні результати та досягнення вітчизняної нейроінформатики. Збірник наукових праць, №8, 8а – НТК, Хмельницький, ВОТТП, с.320-324. 2001.

3.        Красиленко В.Г. та інші. Еквівалентнісна модель гетероасоціативної пам’яті та результати її моделювання. Науково-методичний збірник матеріалів 8НПК ВСЕі УУ – 2008. – с.116-118.

4.        Красиленко В.Г. та інші. Дослідження динамічних процесів в нейромережах за допомогою еквівалентнісних системних енергетичних функцій. Збірник наукових праць, вип.№8, 2001, ВНТК ВОТТП – 2001, с.325-330.

5.        Krasilenko V.G., Nikolsky A.I., Pavlov S. The associative 2D-memories based on matrix-tenzor equivalental models / Радіоелектроніка, Інформатика, Управління, №2(8), 2002, с.45-54.

6.        Krasilenko V.G. et al., The family of new operations “equivalency” of neuro-fuzzy logics, their optoelectronic realization and applications, // SPIE, Vol. 4732, 2002, pp.106-120.

7.        Krasilenko V.G. et al., Creation opportunities for optoelectronic continuous logic neural elements which are the universal circuitry macrobasis of optical neural networks, // Proc. SPIE 2647, pp.208-217.

8.        Krasilenko V.G. et al., The concept of biologically motivated time-pulse information processing for design and construction of multifunctional devices of neural logic, // Proc. SPIE Vol.5421, -2004.- pp.183-194.

9.        Krasilenko V.G. et al., Design of time-pulse coded optoelectronic neuronal elements for nonlinear transformation and integration // Proc. SPIE, Vol. 6974. -2008.- pp.286-297.

10.   Krasilenko V.G. et al., Design and applications of family of optoelectronic photocurrent logical elements on the basis of current mirror and comparators. // Proc. SPIE, Vol. 5948, -2005.- pp.426-435.