Карачун В.В., Мельник В.М.

Національний технічний університет України «КПІ»

ПЕРЕМІЩЕННЯ ТІЛА В РІДИНІ ЗА МИТТЄВОЇ ДІЇ ЗБУРЮЮЧОГО ЧИННИКА

Розглядаємо об’єкт як абсолютно тверде тіло довільної геометричної форми. За цих умов, буде мати місце не тільки поступальний рух, але і кутовий, відносно всіх трьох осей. Для шести невідомих можна побудувати лінійну алгебраїчну систему, коефіцієнти якої будуть залежати від 21 коефіцієнта приєднаних мас і статичних моментів мас.

Припустимо, що абсолютно твердий підводний апарат масою М знаходиться в реальній, для спрощення нестисливій, рідині. Функції, які визначають переміщення середовища і його взаємодію з об’єктом, мають вигляд:

де – приєднана маса; – коефіцієнт тертя; – дельта-функція Дірака, яка представляє миттєве значення імпульса збурюючого чинника і має наступні властивості:

або

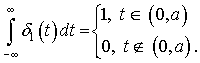
Причому,

де – одинична функція Хевісайда. Зв'язок між функціями Дірака і Хевісайда визначається залежністю

При цьому,

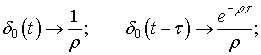
Мають місце наступні рівності:

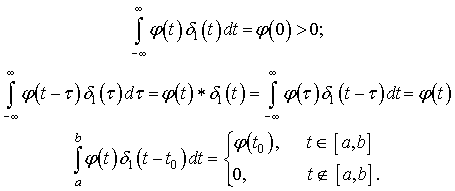
Наведені співвідношення дозволяють з’ясувати закономірність руху підводного апарату. Отже, за урахування тільки тертя при переміщенні човна, диференціальне рівняння руху набуває вигляду:

Перетворимо його:

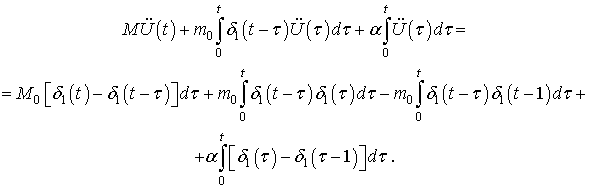
Застосувавши тепер перетворення Лапласа, за нульових початкових умов, отримаємо:

Наведемо першу дріб у вигляді –

Тоді

Цей вираз дозволить визначити коефіцієнти А, В, С:

З урахуванням обчислених значень, маємо:

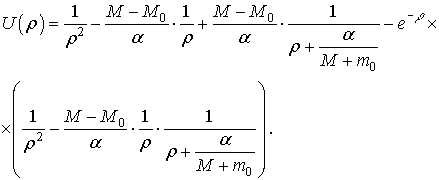
Позначимо

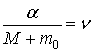
і перейдемо до оригіналу:

Таким чином, розв’язання вихідного диференціального рівняння набуде вигляду:

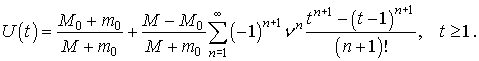
Цей результат співпадає з формулою, яку одержав В.В. Новожилов.

З наведеного походить, що за досить малого тертя і досить великого Т , за період часу переміщення підводного апарату буде цілком окреслюватися першим доданком цієї формули, тобто

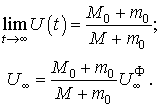
Цей висновок обумовлений тим фактом, що за одиничного зміщення

для узагальненої сили в реальній рідині має місце рівність

З плином часу , переміщення тіла зменшується, якщо . І, навпаки, збільшується, якщо .

Можна задачу розширити, обмеживши стан тіла в’яззю.