Мельник В.Н., Карачун В.В., Ковалец О.Я., Бабаев Р.Н.

Национальный технический университет Украины «КПИ»

О ДОПОЛНИТЕЛЬНОЙ ПОГРЕШНОСТИ ДВУХСТЕПЕННОГО ГИРОСКОПА ПРИ ЦИРКУЛЯЦИИ ОБЪЕКТА В АКУСТИЧЕСКОЙ СРЕДЕ

Запишем дифференциальное уравнение возмущенного движения прибора в форме:

, (1)

где ; ; - моменты инерции поплавка; - полярный и экваториальный моменты инерции ротора; - соответственно коэффициент жесткости пружины и коэффициент демпфирования.

Рассмотрим частный случай. Пусть , и акустическое давление . Нетрудно установить связь между установившимся значением угла поворота поплавка , угловой скоростью вращения РН вокруг оси чувствительности и проникающим акустическим излучением. Из уравнения (1) в этом случае получаем:

(2)

где:

(3)

; (4)

;

- давление в падающей звуковой волне; - круговая частота акустической волны.

С учетом (4), выражение (2) приобретает вид:

. (5)

Или так:

. (6)

Отсюда находим зависимость между установившимся значением угла поворота поплавка и угловой скоростью вращения вокруг оси чувствительности:

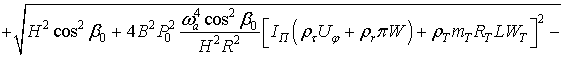
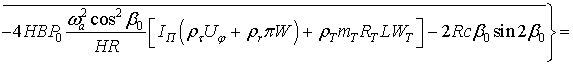
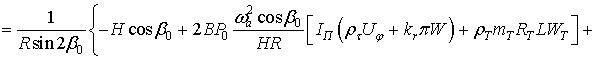
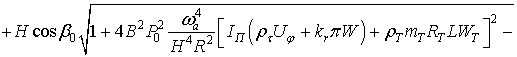
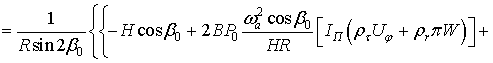
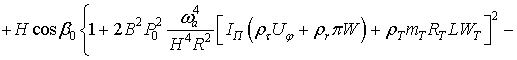
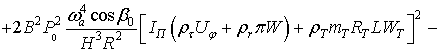
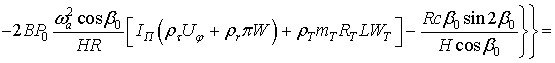
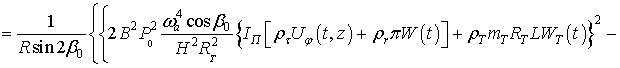
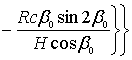. (7)

В том случае, когда проникающее акустическое воздействие отсутствует (для этого в формуле (7) надо положить и ), для малых углов получаем известную формулу, определяющую связь между установившемся углом поворота поплавка и постоянной входной величиной :

. (8)

В противном случае, в формуле (4.17) добавляется еще одно слагаемое, то есть:

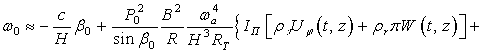
(9)

Именно второе слагаемое здесь учитывает влияние акустического излучения на погрешность прибора при постоянном значении входной величины . В выражении (9) есть закон изгибного движения торца поплавка под действием проникающего акустического излучения.