Желонкин А.И., д.т.н.

Московский государственный открытый университет, Россия

Математическое моделирование диффузионного преобразователя

Перспективность диффузионных преобразователей, построенных на высоко обратимых окислительно-восстановительных системах, обусловлена, физико - химическим процессами, происходящими в жидком теле с малыми значениями сдвиговых напряжений (10^–3 н/м²) высокой концентрацией электропроводящих и электроактивных компонентов (до 10²⁷ 1/м³ и 10²⁶1/м³ , соответственно), благодаря чему маломощный входной механический сигнал управляет в 10⁴...10⁶ раз более мощным выходным электрическими сигналами. Следует отметить, что такое усиление осуществляется в инфранизкочастотном диапазоне, где преобразование сигналов, в частности колебательных механических процессов малого энергетического уровня, представляет значительные трудности [1].

Принцип работы диффузионных преобразователей (ДФП) основан на изменении концентрации электроактивных компонентов электролита в приэлектродных слоях раствора. Уравнением, определяющим потенциал на границе электрод-раствор, в зависимости от концентрации окисленной С_о и восстановленной С_в форм, является соотношение Нернста:

;

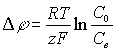где: Dj – скачок потенциала; R – универсальная газовая постоянная; Т – абсолютная температура; z – число электронов, принимающих участие в реакции или валентность электродной реакции; F – число Фарадея.

Величина тока, протекающего через такой преобразователь, зависит от природы реагирующих частиц, состава и концентрации электролита, приложенного напряжения, способов подачи и отвода реагентов J_i к поверхности электродов и других факторов. Важную роль при этом играют процессы переноса вещества, главным образом, диффузии, конвекции и миграции:

первое слагаемое – диффузионный поток концентрации С_i ; второе – миграционный поток (Е – электрическое поле внутри объема электролита,

m – динамическая вязкость); третий – конвективный поток (v – скорость движения электролита).

Статическая вольт-амперная характеристика ДФП, полученная на основании уравнения Тафеля [8], может быть представлена в виде:

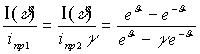; (1)

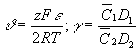где:; (2)

– предельные токи при положительном (J >0) и отрицательном (J <0) напряжениях, соответственно; l – длина электродного канала; e = j ± j(t) – отклонение потенциала электрода от его равновесного значения (т.е. потенциал при i(t) = 0; C₁ =_; C₂ = ), причем равновесное значение потенциала:

;

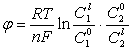Экспериментальные и расчетные вольт-амперные характеристики позволяют определить следующие параметры:

1) Ток преобразователя в интервале J₂ £ J £ J₁, когда ток не достигает предельного значения:

(3)

здесь n = i/i_пр1, m = i/i_пр2 – заданные отношения, не превышающие единицы. Так, при g =0,1 и m = n = 0,9 из выражения (3) находим: J₁ = 1,2; J₂ = –2,3. Величина тока при J_n =1/2 lng : i_n = i_пр1 (g –1)/2J = i_пр2(g –1)/2;

2) Предельные токи i_пр1 и i_пр2 определяют соотношение между концентрациями окислителя и восстановителя: g = i_пр1/ i_пр2 = C_ок/C_восс.

3) Импеданс преобразователя:

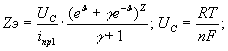при ; .

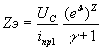4) Крутизну характеристики преобразователя:

;

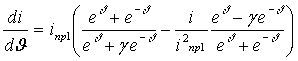максимальное значение которой (Jn = 1/2 lng) равно:

, а при J=0 :

; (4)

Таким образом, крутизна характеристики при J=0, Jn = 1/2lng определяется величинами предельных токов и параметром g. Экспериментально крутизна

определяется в точке J=0, а именно:, Di – вариации тока, соответствующие изменениям напряжения DJ около точки J=0.

Полученные уравнения позволяют рассчитать основные характеристики диффузионного преодразователя.

Литература

1. Желонкин А.И. Математическое моделирование конвективных процессов электрохимических преобразователей // Технология приборостроения. – 2006. №4. – С.35–40.

2. Желонкин А.И. Динамические процессы молекулярно - электронного преобразователя (МЭ) с конвективным переносом заряда // Измерительная техника. – 2008. № 1. – С. 12–18.