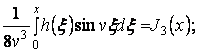Мельник В.Н., Кладун Е.А., Карачун В.В.

Национальный технический университет Украины «КПИ»

ОСОБЕННОСТИ УПРУГОГО ВОЗДЕЙСТВИЯ КРУГОВОЙ

ОБОЛОЧКИ С ПРОНИКАЮЩИМ ЗВУКОВЫМ ИЗЛУЧЕНИЕМ

Вопросы воздействия проникающего акустического излучения маршевых двигателей РН на навигационное оборудование, в частности, и командно-измерительный комплекс изделия, в целом, остаются актуальными и до конца так и не разрешенными.

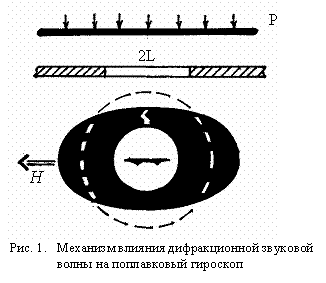
Представляет интерес изучение такой схемы трансляции акустического поля, когда звуковая волна попадает на прибор вследствие дифракции на щели (рис.1). Для конкретности будем изучать это явление на примере серийно выпускаемого промышленностью датчика угловых скоростей класса ДУСУ. Техническая реализация такого прибора представляет собой систему двух коаксиальных круговых цилиндров, разделенных тяжелой жидкостью. Наружный цилиндр будем считать упруго-податливым, а внутренний – абсолютно твердым.

Уравнение наружной оболочки в случае нормального падения звуковой волны имеет вид [1]:

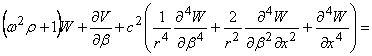
, (1)

Представим искомые функции в виде рядов Фур’є по переменной :

;

;

. (2)

Подстановка их в исходные уравнения (1) дает:

;

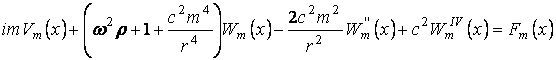, (3)

.

В случае, если из первого уравнения системы (1) имеем:

;

; (4)

.

После подстановки (4) во второе уравнение системы (1), получаем для функции уравнение шестого порядка:

. (5)

Характеристический полином записывается в виде:

, (6)

где .

Рассмотрим случай, когда на мнимой оси находятся два трехкратных корня этого уравнения.

Анализируемая картина наблюдается тогда, когда уравнение (6) имеет трехкратный отрицательный корень

. (7)

Найдем реакцию однородной динамической системы на единичный импульс

, (8)

где - постоянные коэффициенты, которые находятся из условий -

(9)

Очевидно, что , а остальные могут быть определены из тождества:

. (10)

Обнуление коэффициентов при четных степенях переменной х приводит к системе

(11)

которая имеет только нулевое решение

.

Сгруппировав коэффициенты при нечетных степенях переменной х , получаем систему трех уравнений относительно трех постоянных :

(12)

Эта система уравнений однозначно разрешима:

Таким образом, устанавливаем, что:

(13)

Реакция однородной динамической системы (5) на единичный импульс в этом случае будет такой -

, (14)

что позволяет построить частное решение неоднородного уравнения (5) в виде:

(15)

Введем обозначения

(16)

и запишем полное решение уравнения (5):

(17)

где - произвольные постоянные.

Чтобы из семейства решений (17) выделить ограниченные на всей оси, необходимо и достаточно выполнение условий:

; ;

; . (18)

Второе и четвертое условия уже встречались ранее, они привели к соотношению. Первое и третье равенство, с учетом приведут к следующему:

, (19)

.

Очевидно, что это условие сохранится, если вместо записать . При выполнении требований (19) определив постоянные соотношениями

, (20)

а постоянные , сохранив произвольными, исчерпаем все семейство решений неоднородного уравнения (4), ограниченное на всей оси:

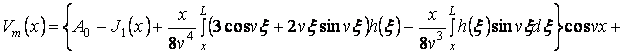
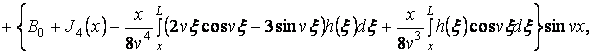
. (21)

Других решений, ограниченных на всей оси , неоднородное уравнение (4) не имеет.

В случае невыполнения условий (19) уравнение (4) не имеет решений, ограниченных на всей оси.

Литература:

1. Kennard E.H. Approximate energy and equilibrium equations for cylindrical shells. J. Appl. Mech., 1956, 23, №4. –Р. 127-132.