Технические
науки /12.Автоматизированные системы управления на производстве.
К.т.н.
Узденбаев Ж.Ш.
Восточно-Казахстанский
государственный технический университет им.
Д.Серикбаева, Казахстан
Построение
системы математических моделей с
использованием
метода динамической идентификации
Как правило, изменение
свойств объекта происходит под воздействием как внешних, так и внутренних
возмущений и их взаимодействий, которые не поддаются измерению и/или аналитическому описанию. И от полноты информации об объекте, во многом зависит степень точности
формализации модели. Под полнотой информации здесь подразумевается также
знание возможных изменений тех или иных динамических свойств объекта и воздействий,
т.е. эти изменения контролируемы и могут быть измерены. Если же они неконтролируемы,
то при определенных допущениях и известных границах неконтролируемых изменений
свойств объекта и воздействий на него в принципе можно обеспечить пониженную (в
пределе - нулевую) чувствительность к этим изменениям желаемых свойств системы
управления. Эти изменения относятся в основном к малым изменениям относительно
расчетных свойств, задаваемых моделью типа "объект - внешняя среда".
В тех случаях, когда нельзя гарантировать "малость" неконтролируемых
изменений свойств управляемого объекта, обычные системы уже не удовлетворяют
требуемым показателям качества или вообще могут стать неработоспособными. Тогда
на основе дополнительной информации о состоянии системы, получаемой с помощью включенных в
первоначальную структуру системы вычислителей, целенаправленно и автоматически
корректируются ее динамические свойства.
При этом задача управления будет считаться решенной, если после
коррекции система вновь удовлетворяет желаемым требованиям и инвариантна к неконтролируемым
возмущениям
[1,2]. Однако на реальнодействующих технологических процессах количество
оцениваемых вышесказанными путями параметров может достичь несколько

десятков, и получить математические описания
каждого канала, а также взаимосвязей этих каналов представляет собой достаточно
сложную задачу [3]. Учитывая вышеизложенное
был разработан рассматриваемый алгоритм.
При этом задача направлена не на определение
зависимостей изучаемой переменной от каждого возмущающего канала, свойств и
взаимодействии этих каналов, а изучается поведение выходной переменной, условно
приняв, что на систему действует некоторый один общий параметр (фактор),
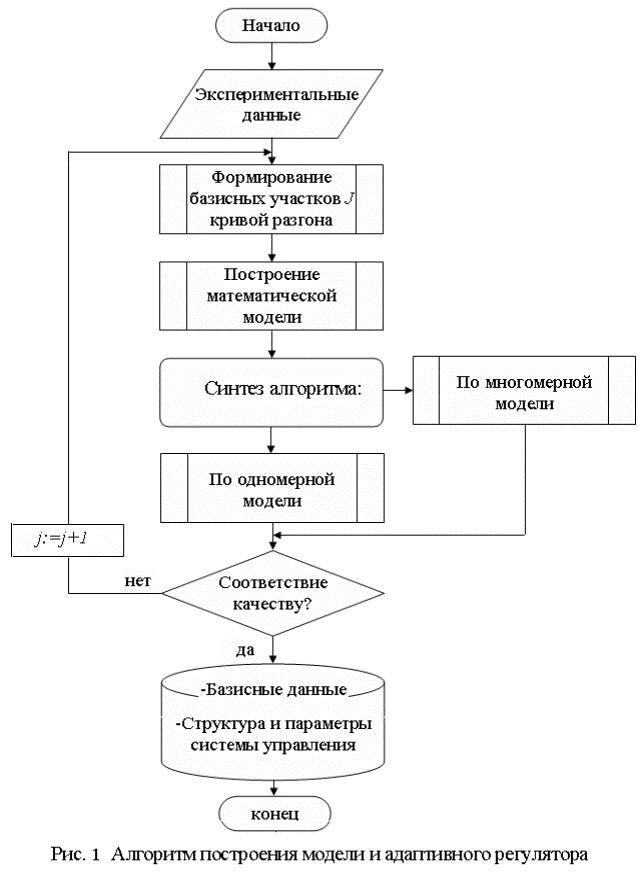
представляющий собой результирующее воздействие возмущающих каналов. Представляемые алгоритмы приведены на рисунках 1 и 2.
Алгоритм формирования базисных участков (серий) кривой разгона рассмотрен в
работе [3,4].
Построение системы математических
моделей кривой разгона осуществляется путем аппроксимаций полученных на
предыдущем этапе базовых линий кривой разгона, с использованием разностного метода Калмана. Метод Калмана является методом динамической идентификации, основан
на результатах эксперимента и позволяет реализовывать цифровые технологий.
Наличие перечисленных, концептуально
важных, с точки зрения рассматриваемой задачи автоматизированного управления,
особенностей, обусловило
применение метода Калмана
при синтезе адаптивного цифрового
алгоритма динамической
настройки параметров систем
автоматического регулирования.
Сущность его заключается в
следующем:
1) в процессе эксплуатации через строго фиксированные
интервалы времени записывают значения входных и выходных параметров;
2) выбирают наиболее простой вид аналитической модели,
записанной в виде разностного уравнения того или иного порядка;
3) по результатам эксперимента и принятого типа модели
методом минимума суммы квадратов отклонений определяют коэффициенты разностного
уравнения;
4) решают разностное уравнение и сравнивают полученные
динамические характеристики с экспериментом;
5) при больших отклонениях задаются разностным уравнением
более высокого порядка и повторяют расчет.
Сопоставление изложенной выше
методики динамической идентификации с порядком выполнения статической
идентификации свидетельствует об их аналогии. Отличие состоит лишь в моделях;
модель в статике описывается алгебраическим уравнением, динамическая модель –
разностным. Для дифференциального линейного уравнения k-го порядка аналогом
будет разностное уравнение вида
![]() (1)
(1)
где n – номер точки эксперимента;
А, В – коэффициенты
разностного уравнения.
Оно и было принято в качестве
исходной модели при динамической идентификации. Поскольку порядок
идентифицируемого объекта вначале неизвестен, процесс получения модели начнется
с наиболее простой модели, а именно – разностного уравнения первого порядка вида
![]() (2)
(2)
Если модель окажется недостаточно
адекватной, следует взять в качестве модели разностное уравнение второго
порядка
![]() (3)
(3)
Далее, используя методику
минимизации суммы квадратов отклонений, т.е. функционала вида
 (4)
(4)
где yEi – экспериментальные значения, yRi – выход модели, будет получена система уравнений
 , (5)
, (5)
из которых можно определить коэффициенты А0, A1,
B0, B1, удовлетворяющие критерию оптимальности.
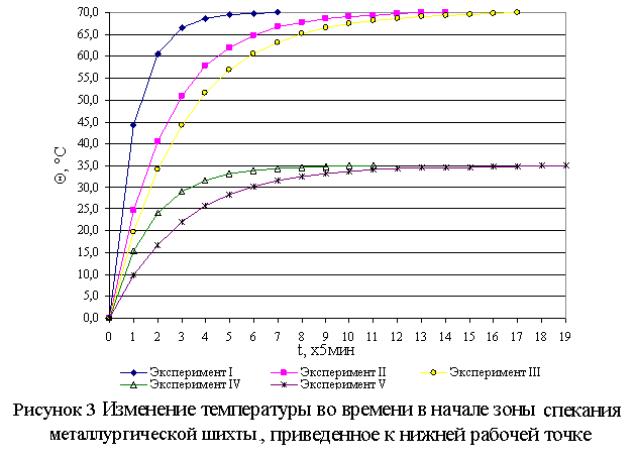
Рассмотрены линий кривой разгона
изменения температуры в начале зоны спекания металлургической шихты, полученную
в процессе измерений с интервалом 5 мин, для различных начальных условий в
рабочем диапазоне от Θb=250
°С до Θе=320 °С и от Θb=250
°С до Θе=285 °С. При измерения использована термопара
ТХК, сигнал с которого поступает в модуль аналогового ввода SM
331-сигнальных
модулей, имеющих внутреннюю встроенную функцию компенсации температуры,
реализуемую путем соответствующей схемы подключения, на базе микроконтроллеров
серии S7 семейства "Simatic". Совокупная погрешность канала
измерения 1,17 % (погрешность измерения самого датчика 1,0%, погрешность преобразования канала
аналогового ввода 0,6 %). Результаты измерений приведены на рисунке 3.
 Для идентификации
опробовано разностное уравнение первого порядка
Для идентификации
опробовано разностное уравнение первого порядка
Θn=A0×Θn-1 +B0×Θе. (6)
Для минимизации суммы квадратов отклонений
будет использован функционал
 . (7)
. (7)
Учитывая уравнение (4.6) и то, что на n-ом шаге выход
модели, получаемое на основе значений предыдущих шагов и коэффициентов А0, B0, должен совпадать с
экспериментальным значением
 . (8)
. (8)
Таким образом, с учетом полученных данных
в результате решения (7), (8) сформирована
следующая система
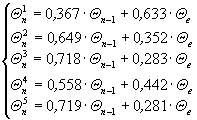 (9)
(9)
При проверке
адекватности моделей исходным данным выявлено, что наибольшее значение
расхождения по результатам пяти экспериментов составило 0,18 %. Совокупная
погрешность с учетом этого составила 1,18%, результируясь с имеющимся значением
1,17%, что свидетельствует о достаточной адекватности модели объекту.
Описание алгоритма управления в
рабочем режиме.
Шаг1. Так как начальные входные условия ещё для определения настроечных
параметров в момент переключения системы в автоматический режим неизвестны, то
при первом запуске система автоматического регулирования настроена на базисный
участок с наибольшим наклоном кривой разгона, с соответствующими параметрами
регулирования [V1], т.к. для данного участка время регулирования является наименьшим по
сравнению с другими базисными участками, соответственно требуется более
оперативные действия по регулированию, т.е. этот базисный участок является
наиболее критичным по фактору времени. Очевидно, такой подход обеспечивает наибольший запас по времени перехода,
условия которого будут описаны ниже, для
крайне правого базисного участка на другие базисные участки.
Шаг2. При выходе значения
регулируемого параметра за зону нечувствительности Yzn система функционирует в режиме
слежения, при котором происходит запоминание значений peгулируемого параметра с заданной
дискретностью. В качестве величины дискретности, позволяющую однозначную
координатную сопоставимость расчетных и реальных значений регулируемого
параметра, выбирается интервал дискретности аппроксимаций кривых разгона, при
котором была обеспечена заданная точность аппроксимаций. В качестве зоны
нечувствительности Yzn выбирается диапазон 3 (по правилу 3-х сигм).
В этом режиме система сравнивает
фактические значения регулируемого параметра с имеющимися в базе данных линиями
кривой разгона. Фактическое значение получается как разность измеренного и
восстановленного, с использованием известной передаточной функций системы
регулирования, значений
Yf
= Ym- Yretr. (10)
Выражение (10) определяет: какие
значения имели бы регулируемый параметр, если бы не было управляющих
воздействии рассматриваемой системы регулирования.
По полученным значениям по формуле
(10) определяется наиболее близлежащая к рассматриваемой базисная линия кривой
разгона, воспользовавшись базой, сформированной в п."Формирование базисных
участков".
Шаг3. При достижении значения регулируемого параметра уровня Yzv – начала зоны регулирования,
система переходит в режим регулирования. Значение Yzv устанавливается исходя из условия
достаточности реакции рассчитываемой
системы за оставшееся время обеспечить требуемые качественные показатели
регулирования. В противном случае осуществляется возврат в п.
"Формирование базисных участков", при этом количество рассматриваемых
линий кривой разгона увеличивается на один. А дальше алгоритм работает в
изложенной выше последовательности.
Если в процессе работы регулятора
появляются оценки значения регулируемого параметра не попадающие в область
кривой разгона, то они заносятся в отдельно созданную базу, а оператору -
технологу выдается соответствующее сообщение. В таких случаях, если данное
событие связано с проявлением неучтенных при составлении области кривой разгона
входных факторов, то область кривой разгона и расчеты параметров настройки пересматриваются,
при необходимости вносятся соответствующие изменения с алгоритмом на рисунке 1.
Выводы
Разработана методика построения
системы математических моделей, позволяющая а) высокую степень адекватности их
экспериментальным данным для непрерывной технологической переменной, в
достаточной степени охватывающий диапазон совокупного изменения входных возмущений; б) упростить процедуру
построения математических моделей и оценить их адекватность на ранней стадии проектирования.
Литература:
1. Сыздыков Д.Ж. Идентификация в системах
управления. Алматы, 2007.
2.
Избранные главы теории автоматического управления. /Андриевский Б.Р., Фрадков
А.Л. - СПб: Наука, 2000.
3.
Мутанов Г.М., Сыздыков Д.Ж., Узденбаев Ж.Ш, КылышкановМ.К. Синтез адаптивных
алгоритмов управления непрерывными технологическими процессами. Монография. Усть – Каменогорск, 2006.
4.
Узденбаев Ж.Ш. Об одном алгоритме построения адаптивной системы управления
непрерывным технологическим процессом. // Сборник трудов международной научно-
технической конференции "Актуальные научные разработки ". София,
Болгария, 2009г.