Карачун В.В., Мельник В.Н.

Национальный технический университет Украины «КПИ»

СИСТЕМАТИЧЕСКИЙ ДРЕЙФ ИНТЕГРИРУЮЩЕГО ГИРОСКОПА ПОД ДЕЙСТВИЕМ N-ВОЛНЫ

Уравнение первого приближения можно записать в виде:

(1)

Или так –

(2)

где - «ложная» угловая скорость и ускорение, обусловленные упруго-напряженным состоянием поверхности подвеса под действием упругой N-волны.

Последние два слагаемых в правой части отображают природу акустического импеданса поплавкового подвеса и дают возможность оценить величину дополнительного дрейфа нуля подвижной части в акустическом поле.

Синхронная качка ЛА:

Частное решение уравнения (2), определяющее влияние акустического излучения в виде осенесимметричной деформации подвеса, имеет вид:

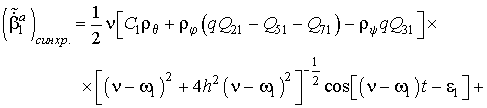
(3)

где

Второе слагаемое пополняет спектр периодических составляющих выходного сигнала. Первое слагаемое при частотах акустического излучения

формирует постоянные составляющие, которые очерчивают систематический дрейф нуля подвижной части.

Асинхронная качка ЛА:

Частное решение уравнения (2) имеет вид:

(4)

Как видно, не только при синхронной, но и при асинхронной качке фюзеляжа имеют место систематические составляющие. Они возникают при наступлении равенств -

т.е. происходит избирательность частот проникающего акустического излучения угловым движением корпуса аппарата вокруг трех осей.

Итак, первое, третье и пятое слагаемые в выражении (4) вносят каждый свою долю в систематический дрейф нуля. Второе, четвертое и шестое – пополняют спектр периодических составляющих.

Систематический дрейф нуля интегрирующего гироскопа будет определяться формулой

где - правая часть выражений (3) и (4).

Таким образом, систематический дрейф нуля прибора под действием проникающего акустического излучения будет следующим:

(5)

(6)

Символ означает осреднение по времени, т.е.