Педагогические науки/5.
Современные методы преподавания
Асканбаева
Г.Б.
Костанайский государственный университет им. А.
Байтурсынова, Казахстан
Применение гомотетии при решении
олимпиадных задач
В обучении математике задачам всегда отводилась достаточно
большая, если не решающая, роль. Задачи становятся не столько целью, сколько
средством обучения. В основном решались типовые, стандартные задачи,
принадлежащие классам алгоритмически разрешимых задач, для которых существует общий метод (алгоритм)
решения. Многообразные ситуации, возникающие на математическом и
нематематическом материале, приводят как к стандартным, так и нестандартным
задачам, алгоритм решения которых либо неизвестен, либо не существует.
Задача считается нестандартной, если для
ее решения требуется применить нестандартные методы решения. Такие виды задач в
основном представляются для решения в математических олимпиадах, которые очень
часто проводятся среди школьников.
Студентам специальности «Математика» в
курсе изучения дисциплин «Элементарная математика», «Практикум по решению математических задач» предлагаются решать задачи повышенной трудности, а также олимпиадные
задачи. Покажем, как теоретический
материал по гомотетии используется при решений олимпиадных задач.
Гомотетией с центром О и коэффициентом 
называется
преобразование плоскости, при котором образом произвольной точки А является
такая точка А/, что 
.
Гомотетию с центром О и коэффициентом k обозначают 
. Единственная неподвижная точка гомотетии (при 
) – ее центр. Если k > 0,
то точки А и А/ лежат на прямой ОА по одну сторону от центра
гомотетии; если k < 0, то разные стороны. При k = - 1 гомотетия есть центральная симметрия. Пусть А/ и В/ -
образы точек А и В при гомотетии с центром О и коэффициентом k. Тогда 
= 
и 
. Следовательно, 
.
Итак, 
. Из этого равенства вытекают важнейшие свойства гомотетии.
По определению произведения вектора на число имеем А/В/ =
Следовательно,
гомотетия с коэффициентом k есть подобие с
коэффициентом 
Гомотетия с
положительным коэффициентом k переводит
каждый луч в сонаправленный с ним луч и, значит, не меняет ориентацию
треугольников. Гомотетия с отрицательным коэффициентом – k может быть представлена в виде композиции гомотетии с
положительным коэффициентом k и поворота на
1800 вокруг центра 
. При этом каждый луч переходит в противоположно направленный
с ним луч, но ориентация треугольников не меняется. С помощью гомотетии решаются разнообразные задачи на построение,
доказательство и вычисление. При этом чаще всего используются следующие
свойства гомотетии:
центр
гомотетии, точка и ее образ лежат на одной прямой;
прямая,
не проходящая через центр гомотетии, и ее образ параллельны;
любые
две окружности гомотетичны, причем если они касаются, то точка касания является
их центром гомотетии [1].
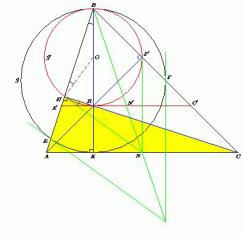
Пример 1.
В остроугольном треугольнике ABC на высоте BK
как на диаметре построена окружность S , пересекающая стороны AB и
BC в точках E и F соответственно. К окружности S в
точках E и F проведены касательные. Докажите, что их точка
пересечения лежит на прямой, содержащей медиану треугольника ABC ,
проведённую из вершины B.
Решение. Рассмотрим гомотетию с центром в
точке B.
При гомотетии с центром в точке B окружность S
переходит в окружность S" , касающуюся окружности S в
точке B . Если при этом точка A переходит в точку A" ,
а точка C – в С , то точки A" и C" лежат
на прямых BA и BC соответственно, касательная AC к
окружности S переходит в касательную A"C" к окружности S"
, медиана BN треугольника ABC – в медиану BN" треугольника
A"BC" . Если мы докажем, что касательные к окружности S"
, проведённые в точках E" и F" , соответствующих
точкам E и F , пересекаются на медиане BN" треугольника
A"BC" , то, рассмотрев обратную гомотетию, получим утверждение
исходной задачи. Пусть H – точка пересечения высот треугольника ABC .
В качестве окружности S" возьмём окружность с диаметром BH и
докажем, что прямая E"N касается окружности S" .
Действительно, поскольку HE" 
AB ,
то CE" – высота треугольника ABC . Тогда 
ABK =
ACE"
, а т.к. E"N – медиана прямоугольного треугольника AE"C
, проведённая из вершины прямого угла, то
NE"C = NCE" = ACE"= ABK = E"BH. Тогда, если O – центр окружности S" , то OE"N = OE"H + NE"C = (90o- OE"B) + E"BH = (90o- E"BH) + E"BH = 90o.
следовательно, NE" – касательная к
окружности S" . Аналогично докажем, что NF" – также
касательная к S" . Таким образом, касательные, проведённые к
окружности S" в точках E" и F" пересекаются
на прямой, содержащей медиану треугольника ABC , проведённую из вершины B
. Следовательно, касательные к гомотетичной S" окружности S ,
проведённые в соответствующих точках E и F , также пересекаются
на этой прямой.
Решение таких задач развивает логическое
мышление, интеллект и формирует характер, в частности, такие его качества, как
настойчивость, упорство в достижении цели, постоянное внимание, способность
сосредоточиться.
Список
литературы
1. Готман. Задачи по планиметрии и методы их решения.
Москва, 1996.
2. Черкасов, А.Якушев. Математика интенсивный курс
подготовки к экзамену (Основные методы решения задач) Айрис-пресс,2003.
3. В.А. Гусев, В.Н.Литвиненко, А.Г.Мордкович. Практикум по решению математических задач (Геометрия). Москва, 1985.