Математика/5. Математическое моделирование

К.т.н. Михеева Т.В.

Алтайский государственный университет, Россия

Математические модели системного компромисса в задачах экономии ресурсов корпоративной производственной системы

В данной работе рассматривается математическая модель системного компромисса [1] экономии ресурсов, являющаяся частным случаем задачи, описанной в [2]. В качестве исследуемого ресурса была выбрана электроэнергия, т.к. планирование и реализация мероприятий энергосбережения в подразделениях производства является важной задачей, решение которой позволит снизить затраты на оплату электроэнергии, а следовательно, снизить затраты на производство продукции и повысить ее конкурентоспособность.

Решение этой задачи состоит из следующих этапов:

1. Разработка энергосберегающих технологий структурных подразделений:

· частично потенциал энергосбережения может быть реализован за счет активности элементов – ;

· частично потенциал энергосбережения может быть реализован мероприятиями центра – .

Тогда, экономия составит .

2. Оценка потенциала энергосбережения каждого подразделения (в рамках выбранных технологий энергосбережения).

3. Реализация энергосберегающих технологий структурных подразделений.

При этом нужно учитывать, что реализация технологий зависит от трудовых и денежных ресурсов, и, следовательно, является:

) ограниченной сверху;

) зависит от информированности и механизма стимулирования (административный механизм – ограничения, экономический механизм – премирование рабочих).

В указанных условиях задача организации функционирования организационной системы может быть записана в виде следующих моделей I и II.

I. Потенциал энергосбережения реализуется за счет активности элементов. Модель основывается на следующих базисных положениях:

1. Подразделение считается активным элементом (АЭ) системы, т.е. оно свободно выбирает размер экономии, который может быть осуществлен на данном производстве за определенный промежуток времени, в пределах . Здесь информированность подразделений о возможном потенциале экономии.

2. Поведение подразделений зависит от трудозатрат в области экономии ресурса, которые можно выразить функцией , зависимой только от активности подразделения и удовлетворяющей специальным ограничениям [3]:

1) при нулевой активности трудозатраты равны нулю: ;

2) при любой ненулевой активности (в пределах от 0 до ) функция трудозатрат положительна: ;

3) функция трудозатрат – монотонно возрастающая функция: , если , т.е. производная функции положительна: ;

4) трудозатраты на фиксированный прирост экономии ресурса возрастают с ростом экономии ресурса, т.е. вторая производная неотрицательна: ;

5) при приближении к максимальному размеру экономии ресурса трудозатраты становятся большими, что математически учитывается следующим условием: .

Примером функции , удовлетворяющей этим условиям, может служить логарифмическая функция [4]:

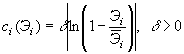. (1)

3. Фонд оплаты экономии ресурсов формируется за счет экономии ресурсов, а плата за экономию устанавливается как доля этого фонда. Оценку оптимальной доли от экономии ресурса определяет работодатель (центр), который принимает решения исходя из собственных экономических интересов и информированности о возможностях подсистем. Т.е. центр устанавливает значение из своих независимых расчетов и сообщает это значение подразделениям.

В указанных условиях задача организации функционирования организационной системы принимает следующий вид.

Математическая модель поведения центра согласно [1] и [2] с учетом описанных условий может быть представлена в виде следующей модели системного компромисса:

(2)

задача подсистем –

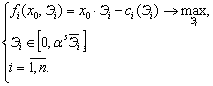(3)

Центр должен определить оптимальное значение , при котором экономия ресурсов подразделений с учетом оплаты труда была бы максимальной. Для этого решается задача типа . Далее необходимо найти для каждого подразделения, то есть долю в сумме экономии затрат на ресурс, при которой подразделение начнет проявлять дополнительную активность.

Если , то стимулирование активности подразделения в области экономии ресурса нецелесообразно, если , то стимулирование может быть целесообразным и в этом случае подразделения, зная значение , находят свои решения из задачи (3).

Решение о целесообразности стимулирования подразделений на экономию ресурсов принимает руководство путем сравнения полученного дохода от экономии этих ресурсов с затратами на организацию системы стимулирования и поддержания ее функционирования (например, на установку приборов учета ресурсов).

II. Потенциал энергосбережения реализуется мероприятиями центра. Модель, когда потенциал энергосбережения реализуется мероприятиями центра, отличается от предыдущей модели тем, что здесь реализация энергосберегающих технологий зависит от трудовых и денежных ресурсов по решениям центра в виде производственной функции Кобба-Дугласа:

,

где – вложенные средства, – трудовые ресурсы, осуществляющие энергосбережение. Значения коэффициентов определяются согласно общепринятой методике, изложенной в работе [5].

Другим отличием является возникновение новой задачи по оценке оптимального распределения указанных ресурсов, ответственным за определение которого выступает центр.

Тогда в указанных условиях задача может быть решена согласно процедурам, приведенным в [2]:

1. нахождение коэффициента ;

2. задача распределения ресурсов.

Практическая значимость результатов исследования заключается в следующем:

1. Предложена новая математическая модель системного компромисса экономии ресурсов, позволяющая с использованием соответствующих данных оперативно корректировать нормы расхода ресурса и оценки информированности подразделений.

2. Проведенный сравнительный анализ результатов, полученных в результате моделирования, с фактическими данными производства позволяет сделать вывод об эффективности использования предлагаемой модели.

3. Данная модель может быть рекомендована при разработке энергосберегающих технологий структурных подразделений предприятия, оценке потенциала энергосбережения каждого подразделения (в рамках выбранных технологий энергосбережения).

Литература:

1. Алгазин Г.И. Модели системного компромисса в социально-экономических исследованиях / Монография. – Барнаул: Азбука, 2009.

2. Алгазин Г. И., Михеева Т. В. Применение игровых имитационных моделей системного компромисса для анализа функционирования корпоративных производственных систем // Совместный вып. журнала «Вычислительные технологии» и журнала «Вестник КазНУ им. Аль-Фараби». Серия: Математика, механика, информатика. Т. 13, Ч. 1, № 3 (58), 2008. Стр. 120-125.

3. Опойцев В.И. Равновесие и устойчивость в моделях коллективного поведения. – М.: Наука, 1977.

4. Оскорбин Н.М. Исследование систем управления. – Барнаул: Изд-во АГУ, 1998.

5. Клейнер Г.Б. Производственные функции. – М.: ГУ-ВШЭ, 2000.