ОБ ОПТИМАЛЬНОЙ ТРАЕКТОРИИ ДВИЖЕНИЯ НИТЕРАСКЛАДЧИКА В ДЕТЕРМЕНИРОВАННОЙ МОДЕЛИ ПРОЦЕССА НАМОТКИ КОНСТРУКЦИЙ ИЗ ВОЛОКНИСТЫХ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ

 

Битюков Ю.И., Калинин В.А.

Московский авиационный институт (государственный технический университет), г. Москва, Россия

 

1. ВВЕДЕНИЕ

Последние десятилетия являются свидетелями все возрастающего применения композиционных материалов в авиастроении и ракетно-космической отрасли. Это объясняется простотой достижения аэродинамических свойств и заданного теоретического контура внешнего обвода летательных аппаратов при изготовлении конструкций из композиционных материалов, небольшим весом, а также возможностью получать монолитные конструкции без швов и скреплений. Одним из недостатков композиционных материалов является до сих пор их высокая стоимость. Поэтому при моделировании процесса изготовления конструкций из композитов методом намотки лентой, составленной из однонаправленных армирующих волокон, пропитанных связующим, которая укладывается на поверхность технологической оправки, необходимо иметь высокую точность соответствующих моделей не только для достижения требуемых параметров конструкций, но и для экономии материалов за счет виртуальной компьютерной отладки процесса изготовления конструкций.

Основным технологическим фактором, регулирующим прилегание ленты к поверхности оправки, является заданное натяжение на раскладчике ленты намоточного станка. Натяжение может быть как постоянным, так и переменным, в зависимости от сложности поверхности технологической оправки, схемы армирования, возможности намоточного оборудования. Обычно стараются задать некоторое среднее значение натяжения ленты, не превышающее максимально допустимую деформацию армирующего материала. Такое натяжение не обеспечивает максимально возможное прилегание ленты к поверхности технологической оправки. При разработке управляющей программы важно знать необходимое натяжение ленты на каждом этапе укладки ленты для формирования правильного закона движения раскладчика ленты. На основе геометрической модели укладки ленты, разработанной в статье [1] и оценки деформации различных волокон ленты можно вывести зависимость для определения величины натяжения, обеспечивающего плотное прилегание ленты к поверхности оправки. Вывод такой зависимости осуществляется в четвертом разделе статьи. Важное значение имеет учет скорости и ускорения протяжки ленты через лентоформирующий тракт намоточного станка. Известно, что скорость и ускорение протяжки ленты оказывают сильное возмущающее воздействие на интенсивность пропитки ленты, а, значит, и на качество изделия.

Работы многих авторов посвящены нахождению оптимальной траектории и закона движения раскладывающего механизма намоточного станка [2-5], но эти законы строятся без учета реальной структуры ленты и рассматриваются только для класса поверхностей вращения. В статье [1] была предпринята попытка построения траектории движения раскладывающего механизма с учетом реальной структуры ленты, но эта траектория строилась без учета ограничений на возможные положения механизма, натяжения нитей ленты, скорости и ускорения протяжки ленты. В данной статье впервые предпринята попытка обобщения существующих результатов по нахождению траектории и закона движения раскладывающего механизма станка с учетом, структуры ленты и описанных ограничений. Кроме того, траектория и закон движения строятся для существенно более широкого класса поверхностей – поверхностей зависимых сечений с криволинейной образующей.

2. ПОСТАНОВКА ЗАДАЧИ

         Пусть в пространстве фиксирована декартова система координат Oxyz. Поверхность технологической оправки S, принадлежащая классу C2 поверхностей зависимых сечений с криволинейной образующей [6], задана параметрическим представлением . Схема укладки ленты задается с помощью гладкой кривой g, имеющей параметрическое представление .

Необходимо переместить нитераскладчик из начального положения в конечное за минимальное время, не нарушая ограничений на натяжения нитей ленты, допустимые положения нитераскладчика, скорости и ускорения протяжки ленты через лентоформирующий тракт.

3. ОГРАНИЧЕНИЯ НА ТРАЕКТОРИЮ ДВИЖЕНИЯ НИТЕРАСКЛАДЧИКА

Положение раскладывающего механизма намоточного станка можно задать, указав радиус-векторы ,  крайних точек A и B механизма (рис. 1). Точки A и B, очевидно, должны принадлежать торсовым поверхностям SA и SB, направляющие которых представляют собой кривые на поверхности, по которым укладываются крайние нити ленты (рис. 1).

5

Рис. 1. Укладка нитей ленты на технологическую оправку

В статье [1] была построена геометрическая модель укладки ленты для любого метода намотки. Как известно, по исходному состоянию укладываемой ленты различают «сухую» и «мокрую» намотки. Для «сухой» намотки используется заранее изготовленная (сформированная из определенного числа нитей, определенной ширины и толщины, подсушенная и смотанная в барабаны) лента. При «мокрой» намотке лента формируется из нитей, пропитывающихся связующим в процессе намотки. В статье [1] любой из видов намотки моделируется единым образом - с помощью явно заданного гладкого отображения прямоугольника в трехмерное Евклидово пространство , где -максимальная ширина ленты при «мокрой» намотке и неизменная ширина ленты при «сухой » намотке. Как и в статье [1], будем предполагать, что выполнены следующие допущения

1. Лента состоит из n идеальных растяжимых однородных нитей.

2. Укладка крайних нитей ленты осуществляется по кривым с параметрическим представлением  и . Укладка произвольной нити, лежащей между крайними, осуществляется по одной из кривых , где  и фиксировано.

Используя вектор-функцию , легко написать параметрические представления торсовых поверхностей [6], которым должны принадлежать крайние точки нитераскладчика. Итак, параметрические представления поверхностей SA и SB имеют вид:

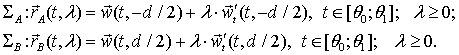
Следовательно, задать положения точек A и B можно указав значения параметров . Обозначим  - значение параметра , определяющее образующую торсовой поверхности SA, которой принадлежит точка A,  - расстояние от точки A до точки касания нити и поверхности. Аналогично обозначим  - значения параметров, определяющие точку B. Выбор таких параметров, конечно, не произволен и должен удовлетворять определенным ограничениям.

Во-первых, расстояние  между точками A и B не может изменяться, поэтому точка B должна принадлежать линии пересечения торсовой поверхности SB и сферы  с центром в точке A и радиусом  (рис. 1). Таким образом, должно выполняться равенство .

Во-вторых, нитераскладчик должен находиться в области  его допустимых положений. Эта область определяется возможностями намоточного станка, и в рассматриваемой модели будет задаваться двумя поверхностями S1 и S2 (рис.1) с параметрическими представлениями . Следовательно, должно выполняться условие , где .

         Рассмотрим теперь ограничения на скорость и ускорение протяжки ленты. Обозначим через , длины протянутых крайних нитей ленты, а . Пусть  обозначает время. Тогда  являются функциями от времени . Обозначим через , первые и вторые производные этих функций по времени. Тогда скорость и ускорение протяжки нити могут быть найдены по формулам

;

Таким образом, должны выполняться неравенства , где  заданные константы.

Натяжения нитей ленты, должны обеспечивать плотное прилегание их к поверхности технологической оправки. Для нахождения следующего ограничения рассмотрим задачу определения натяжения нитей ленты.

 

4. ОПРЕДЕЛЕНИЕ НАТЯЖЕНИЯ НИТЕЙ ЛЕНТЫ В ПРОЦЕССЕ ЕЕ УКЛАДКИ НА ТЕХНОЛОГИЧЕСКУЮ ОПРАВКУ

Рассмотрим произвольную нить, укладываемую по кривой . В каждой ее точке имеется натяжение. При равновесии нити на оправке, натяжение будет функцией параметра . Таким образом, натяжение нити, укладываемой по кривой , описывается функцией  ( фиксировано). Мы будем рассматривать упругие деформации нитей. Тогда натяжение связано с относительным удлинением нити законом Гука и, как видно из [1], его можно найти по следующей формуле

,

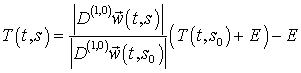где  произвольное фиксированное значение, а E – модуль упругости материала нити. Итак, натяжение  произвольной нити ленты выражается через натяжение  одной из ее нитей.

Пусть лента состоит из n нитей, укладываемых по кривым , . Так же, как и крайние точки A,B нитераскладчика, точка схода Ai i-ой нити (A1=A, An=B) принадлежит торсовой поверхности . Пусть  - значение параметра , определяющее образующую торсовой поверхности , которой принадлежит точка Ai. Очевидно, что при выбранных , значения ,  не могут быть выбраны произвольно. Так как нити должны быть в натянутом состоянии, то значения  должны быть выбраны из условия пересечения торсовой поверхности  и отрезка AB. Таким образом, значение  находится из уравнения

,

где , а . Заметим, что данное векторное уравнение равносильно системе трех уравнений с тремя неизвестными, две из которых могут быть легко исключены (так как входят в систему линейным образом). Поэтому решение такого уравнения можно легко свести к решению методом дихотомии нелинейного уравнения с одним неизвестным.

         Ленту обычно наматывают с некоторым технологическим натяжением  (здесь  - разрывная нагрузка арматуры ленты), установленным на раскладчике ленты намоточного станка. Тогда натяжение  является некоторой функцией технологического натяжения. Суммарное натяжение нитей ленты имеет вид:

Условие плотного прилегания нитей ленты к поверхности выражается следующими неравенствами:

Итак, условие плотного прилегания нитей ленты к поверхности, выраженное предыдущими неравенствами есть дополнительное ограничение на траекторию движения нитераскладчика и значения натяжения . Для упрощения, дальнейших уравнений, будем считать, что

.

5. МОДЕЛЬ ОБЪЕКТА УПРАВЛЕНИЯ

         Объектом управления является нитераскладывающий механизм. Обозначим

.

Тогда, если  - время перехода нитераскладчика из состояния, в котором он находился в момент времени , в состояние, в котором он оказывается в момент времени . Тогда справедливы приближенные равенства

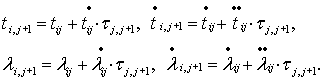
Следовательно, должны выполняться равенства

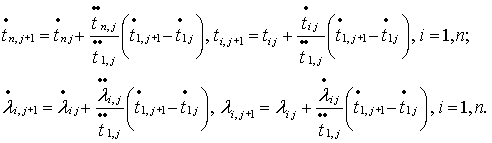
Таким образом, вектор состояния нитераскладчика имеет вид , где , а поведение объекта управления можно описать разностным уравнением

, ,

где  - вектор управления, а

.

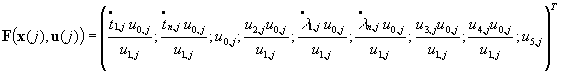Обозначим . Суммируя сказанное в разделах 3 и 4, можно заключить, что множеством допустимых состояний нитераскладчика является пересечение множеств

;

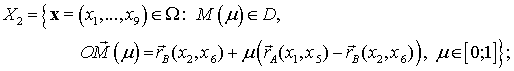
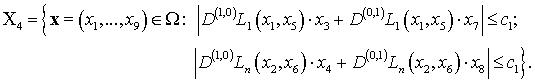
Множеством допустимых управлений служит следующее множество

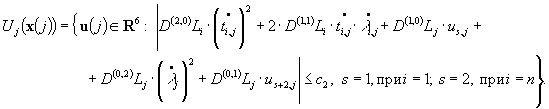
Время перехода  из состояния  в состояние  может быть найдено следующим образом . Эффективность всего процесса в целом будем характеризовать функцией вида:

,

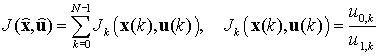где  - набор состояний (фазовая траектория процесса), а  - набор векторов управления. Итак, оптимальный закон движения нитераскладчика (оптимальный в смысле увеличения производительности процесса за счет сокращения времени изготовления конструкции) может быть найден в результате решения следующей задачи многошаговой оптимизации, которая может легко быть решена методом дискретного динамического программирования:

Работа выполнена при финансовой поддержке ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009-2013 годы по теме «Развитие теории геометрического моделирования технологических процессов намотки и выкладки конструкций из волокнистых композиционных материалов», Госконтракт № 14.740.11.0279 от 17 сентября 2010 года.

ЛИТЕРАТУРА

1. Битюков Ю.И., Калинин В.А. Численный анализ схемы укладки ленты переменной ширины на технологическую оправку в процессе намотки конструкций из композиционных материалов //Механика композиционных материалов и конструкций.–2010.–Т.16.-№2.-С. 276-290.

2. Князев Д.Н. Математические модели и алгоритмы программирования процессов формообразования изделий методом намотки: автореф. дис. канд. техн. наук: 05.13.18 / Д.Н. Князев. – Новочеркасск, 2002.

3. Маринин В.И., Городецкий Г.Б. Задача расчета оптимальных по быстродействию траекторий и законов движения исполнительных органов намоточных станков с программным управлением // Системы управления технологическими процессами: Сб. ст. Новочеркасск, Изд. НПИ, 1976, Вып. 3.

4. Задача оптимизации законов движения исполнительных органов многокоординатных станков с программным управлением / В.В. Алексейчик, В.К. Ершов, А.Н. Иванченко, Я.Я. Чикильдин. - В кн.: Системы управления технологическими процессами. Новочеркасск, 1976, с. 51-54.

5. Разработка программно-математического обеспечения многокоординатных намоточных станков // В.В. Алексейчик, Ф.Г. Душенко, В.К. Ершов, А.Н. Моргун, Я.Я. Чикильдин. - Системы управления технологическими процессами: Сб. ст. Новочеркасск: Изд. НИИ, 1976, Вып. 3.

6. Иванов Г.С. Начертательная геометрия: Учебник для вузов / Г.С. Иванов. - М.: Машиностроение, 1995. - 224 с.