Технические науки/12. Автоматизированные системы управления на производстве

Абидова Е.А., к.т.н. Пугачёв А.К., к.т.н. Пугачёва О.Ю., д.т.н. Чернов А.В.

Волгодонский инженерно-технический институт НИЯУ МИФИ

Диагностика электроприводного оборудования по амплитудно-фазовым характеристикам сигнала тока двигателя

Особенностью асинхронных двигателей (АД) является малая величина воздушного зазора (ВЗ) между статором и ротором. Надежность АД во многом зависит от симметрии зазора, которая может нарушиться в результате многих причин (пульсация питающего напряжения, короткое замыкание витков обмотки, механических дефектов). В настоящей работе предлагается рассмотреть влияние механических дефектов привода на неравномерность ВЗ, как наиболее сложного фактора, связанного с нелинейным преобразованием механических колебаний в электромагнитные.

Известно, что в результате дефектов в механической части привода наблюдается пульсация скорости вращения вала ротора[1]. Покажем, как отклонения скорости вала отражаются на состоянии двигателя.

Рассмотрим обобщенную электрическую машину с одной парой полюсов и двумя обмотками на статоре и роторе. Все величины, относящиеся к обмотке статора, имеют индекс D; поперечной оси индекс Q; для обмоток ротора по продольным и поперечным осям используются индексы d и q [2].

Положим, что обмотке статора D протекает ток i_D, создающий магнитный поток в положительном направлении оси d, и ротор вращается против часовой стрелки. При этом в обмотках D и d индуцируются наведенные ЭДС:

где p=d/dt оператор дифференцирования.

В обмотке ротора q индуцируется ЭДС вращения, пропорциональная угловой скорости ротора ω_р:

Аналогичные выражения можно получить для ЭДС в обмотках машины от остальных токов. В обмотках D и Q индуцируется только наведенная ЭДС:

Суммарная ЭДС в обмотках d и q содержит как наведенные ЭДС, так и ЭДС вращения:

Приложенные к обмоткам машины напряжения равны сумме напряжений на активных сопротивлениях и противо-ЭДС:

Эту систему уравнений можно записать в матричном виде

; (1)

где матрицы напряжений, токов и полных сопротивлений обобщенной машины имеют вид

D Q d q

u=; i=; Z=. (2)

Матрица Z представляет собой сумму трех матриц:

(3)

Матрица R – матрица сопротивлений; L – матрица индуктивностей; G – так называемая матрица момента.

Матрица сопротивлений R содержит четыре сопротивления обмоток:

D Q d q

Z=.

Матрица индуктивностей L содержит все само- и взаимные индуктивности обмоток:

D Q d q

L=.

Матрица G содержит взаимные индуктивности обмоток, возникающие вследствие вращения ротора:

D Q d q

G=. (4)

Уравнение для напряжений (4) запишем в виде

(5)

Где вектор индукции

В=Gi=.

Для асинхронных машин p=jω, а токи и напряжения – комплексные временные векторы. Тогда матрицу сопротивлений можно записать в виде

(6)

Здесь матрица индуктивных сопротивлений

D Q d q

X=.

Матрица сопротивлений для момента

D Q d q

ωG=.

υ =ω_р/ω_с – скорость ротора в долях асинхронной скорости; x_D, x_Q, x_d, x_q–индуктивные сопротивления обмоток машины, соответственно обмоток D, Q, d и q; причем

где x_Ds, x_Qs, x_s – индуктивные сопротивления рассеяния обмоток, а x_md и x_mq – сопротивление взаимной индукции.

Матрицу сопротивлений можно записать в виде

D Q d q

Z=. (5)

Составляющими векторов тока и напряжения будут комплексные временные векторы

=; =; (6)

В частном случае двухполюсной машины с одинаковыми собственными параметрами обмоток статора Z_S.

Уравнения ЭДС контуров АД запишем в виде

D Q d q

Χ=, (7)

Исключая из уравнений токи короткозамкнутого ротора и , придем к системе уравнений относительно токов и :

Χ=. (8)

Здесь

;

Решая уравнения относительно одного из токов статора получаем

. (9)

Таким образом, пульсация скорости ротора вызывает модуляции тока статора частотой вращения ротора.

Выполненный анализ пространственно-временных гармоник магнитного поля в ВЗ АД при несинусоидальном токе показывает, что даже незначительные искажения тока статора может стать причиной значительной вибрации, а, следовательно, неравномерности ВЗ [3].

При токе статора, насыщенном гармоникам неравномерно вращающегося ротора (10), в двигателе возникает множество просторанственно-временных гармоник поля и тока.

(10)

Наиболее сильными из гармоник являются волны линейной токовой нагрузки вида

(11)

и волны индукции вида
(12)

Где A_1k –амплитуда линейной плотности k-й гармоники тока статора; B_��k – амплитуда индукции k-й гармоники результирующего поля в ВЗ; р – число пар полюсов; �� – координата в ВЗ.

В результате взаимодействия поля и тока возникает радиальная и тангенциальная вибрация. Радиальная вибрация будет возбуждаться силой

(13)

Тангенциальная – силой

(14)

Принимая во внимание, что радиальные колебания статора значительно меньше изгибных колебаний с таким же числом волн, возбуждаемых тангенциальными силами, можно считать, что неравномерность ВЗопределяется действием тангенциальной силы.

Рис. 2 – Деформации статора, вызываемые тангенциальными силами в воздушном зазоре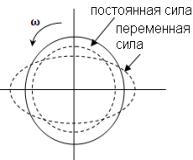

Из выражения (14) видно, что значение тангенциальной силы зависит от разности фаз гармоник тока. При суммировании кратных гармоник может возникнуть постоянная составляющая, которая усугубляет неравномерность ВЗ. То есть на каждую элементарную площадку статора действует

постоянно направленная тангенциальная сила p_��0 и переменная тангенциальная сила p_��1, имеющая синусоидальное распределение по окружности расточки статора (рис. 2) [4].

Рис. 3 – Изменение постоянной составляющей в зависимости от разности фаз между гармониками

Н/см²

Величина постоянной составляющей определяется разностью фаз между гармониками (рис.3). Положительное значение постоянной составляющей силы говорит о том, что сила сжимает статор, отрицательное – сила работает на растяжение.

Спектральный анализ, применяемый для оценки амплитудно-частотного состава электрических и виброакустических сигналов, не позволяет оценить разность фаз между компонентами сигнала. То есть одинаковые спектры могут соответствовать как удовлетворительному состоянию двигателя, так и критическому состоянию, связанному с действием тангенциальной силы. В настоящей работе для оценки разности фаз предлагается использовать амплитудно-фазовые характеристики (АФХ). АФХ сигнала, состоящего из двух кратных гармоник, сдвинутых друг относительно друга на некоторую разность фаз представляет собой фигуру называемую улиткой Паскаля (рис. 4) [5].

Рис. 4 – АЧХ полигармонического сигнала при разности фаз π /2 (а) и π(б)

б

а

Положение оси симметрии данной фигуры позволяет оценить разность фаз между гармониками и, сделать вывод о величине и направлении действия постоянной составляющей тангенциальной силы.

Для определения влияния различных механических дефектов на состояние двигателя, с точки зрения нарушения равномерности ВЗ, были проведены ряд экспериментов на лабораторной установке. Имитировались разные степени дефекта червяка редуктора (постепенно подтачивался зуб червяка). Были получены АФХ кратных гармоник ротора по сигналам, снятым с обмоток статора электродвигателя (рис.5). При развитии дефекта наблюдался рост амплитуд и числа гармоник ротора, смещение фаз между гармониками. При наибольшем развитии дефекта между гармониками устанавливается сдвиг фаз близкий к ��/4. Постоянная составляющая силы, вызывающей деформации статора в этом случае максимальна.

б

в

а

Рис. 5 – АФХ по сигналам, снятых с обмоток статора электродвигателя: начальная стадия дефекта червячного колеса (а), развитие дефекта червячного колеса (б), развитый дефект червячного колеса(в).

Таким образом, рекомендуется при диагностике электроприводного

оборудования, если в спектре сигнала обнаруживаются кратные гармоники, характеризующие механический дефект привода, проводить дополнительный анализ АФХ гармоник сигнала.

Литература:

1. Биргер И.А., Техническая диагностика. – М.: Машиностроение, 1978. – 240 С.

2. Коллакот Р.А. Диагностирование механического оборудования: Пер. с англ./ Под ред. Ю.Н. Мясникова – Л.: Судостроение, 1980. 296 С.

3. Григорьев Н.В. Вибрация энергетических машин. – Л.: Машиностроение, 1974. – 464 С.: ил.

4. Шубов И.Г. Шум и вибрация электрических машин. – Л.: Энергоатомиздат, 1986. – 208 С.: ил.

5. Цифровая обработка сигналов: справочник/Гольденберг Л.М., Матюшин Д.Б., Поляк М.Н. – М.: Радио и связь, 1985. – 312 С.