Гусарова О.В., асп.,
Ружинська Л.І., к.т.н.,
проф.
Національний технічний
університет України „КПІ”
Математична модель процесу концентрування біологічно активних речовин (бар)
упарюванням
Розглянемо плівкову течію
розчину БАР по зовнішній поверхні вертикально розташованої труби (рисунок 1).
Позначимо зовнішній діаметр труби - dн,
висоту труби L. До зовнішньої
поверхні труби підводиться теплова енергія з інтенсивністю q, Вт/м2. Із зовнішньої поверхні плівки відбувається
випарювання розчину БАР.

Рисунок
1- Плівкова течія розчину БАР по зовнішній поверхні вертикально розташованої
труби з урахуванням випарювання розчину
Розташуємо початок
системи координат у верхньому перерізі труби. Товщина плівки δ на порядок
менше радіуса труби. З точки зору процесів гідродинаміки та теплообміну задача
осесиметрична, та може розглядатися в пласкій системі координат xOz, причому вісь z співпадає з віссю труби,
а вісь х направлена перпендикулярно
стінці труби.
Запишемо загальноприйняту
математичну модель, яка складається з
- рівняння руху Нав'є -
Стокса
 , (1)
, (1)
де ![]() ,
, ![]() - густина та
в'язкість розчину БАР відповідно,
- густина та
в'язкість розчину БАР відповідно, ![]() - прискорення
вільного падіння,
- прискорення
вільного падіння, ![]() - час,
- час, ![]() ,
, ![]() - швидкості вздовж
осей z та х відповідно,
- швидкості вздовж
осей z та х відповідно, ![]() - гідростатичний
тиск.
- гідростатичний
тиск.
- рівняння енергії
![]() , (2)
, (2)
де ![]() ,
, ![]() - теплоємність та
теплопровідність розчину БАР відповідно,
- теплоємність та
теплопровідність розчину БАР відповідно, ![]() - температура.
- температура.
Розглядаємо встановлений ламінарний
режим течії плівки.
![]() .
.
Враховуючи, що ![]() , приймаємо
, приймаємо ![]() . Сила інерції значно нижче сили тертя та тяжіння. Гідростатичним
тиском нехтуємо (плівка тонка).
. Сила інерції значно нижче сили тертя та тяжіння. Гідростатичним
тиском нехтуємо (плівка тонка).
Запишемо рівняння руху (1)
в проекції на вісь z з урахуванням допущень
та спрощень
![]() . (3)
. (3)
Граничні умови
на поверхні стінки:
- при ![]() ,
, ![]() ,
,
на поверхні плівки:
- при ![]() ,
, ![]() .
.
Інтегруючи рівняння (3),
отримаємо
![]() , (4)
, (4)
![]() , (5)
, (5)
- при x=0, С2=0,
- при x=δ, ![]() .
.
Підставивши постійні
інтегрування в рівняння (5) отримаємо
 . (6)
. (6)
Вводимо нову змінну ![]() (безрозмірна
координата).
(безрозмірна
координата).
Тоді
 . (7)
. (7)
Для визначення безрозмірної
координати ![]() необхідно знайти
товщину плівки δ та задатись значеннями швидкості
необхідно знайти
товщину плівки δ та задатись значеннями швидкості ![]() .
.
Визначимо товщину плівки
із рівняння матеріального балансу.
Знайдемо кількість
розчину
![]() . (8)
. (8)
де ![]() - витрата розчину в
кожному перерізі по висоті труби, тому позначимо
- витрата розчину в
кожному перерізі по висоті труби, тому позначимо ![]() =f(z).
=f(z).
З урахування
випаровування розчину ![]() на висоті z
на висоті z
![]() ,
,
тоді рівняння (8) буде
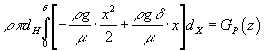 . (9)
. (9)
Проінтегруємо та перетворимо
рівняння (9)
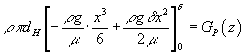 ,
,
![]() .
.
Звідси товщина плівки
буде
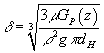 . (10)
. (10)
тоді підставивши рівняння (10) у
рівняння (7) отримаємо
 . (11)
. (11)
Позначимо
 . (12)
. (12)
Підставивши (12)
у рівняння (11) отримаємо
![]() , (13)
, (13)
враховуючи, що ![]() - відомі,
- відомі, ![]() , при
, при ![]() -
- ![]() , при
, при ![]() -
- ![]() ,
, ![]() (при
(при ![]() ).
).
Тоді з (13)
 .
.
Знаючи масив
значень ![]() , ми можемо знайти х. При відомих
, ми можемо знайти х. При відомих ![]() та х (довжина пробігу частинки) можна
знайти час перебування розчину на певній довжині труби.
та х (довжина пробігу частинки) можна
знайти час перебування розчину на певній довжині труби.
Записавши
рівняння енергії (2) через безрозмірну координату, ми отримаємо
 .
.
Таким чином
ми отримали температуру як T=f(z, η). Розв'язавши це рівняння
аналітичними методами, отримаємо масив значень T.
Активність
БАР залежить від часу перебування розчину в апараті, тобто від часу обробки та
температури. Із збільшенням часу перебування розчину в апараті втрачається його
активність. Із збільшенням температури відбувається руйнація (загибель) БАР.
Тому це необхідно враховувати в математичній моделі.
Знаючи
температуру та час перебування розчину в апараті ми можемо ввести в загальноприйняту
математичну модель рівняння залежності активності розчину від цих величин.
Тоді
активність розчину буде
![]() , (16)
, (16)
де ![]() - значення активності
до обробки,
- значення активності
до обробки, ![]() - енергія активації,
- енергія активації, ![]() - універсальна газова
стала.
- універсальна газова
стала.
Для перевірки
математичної моделі необхідно розрахувати значення активності розчину по
математичній моделі і порівняти їх з отриманими експериментальним шляхом. Якщо
значення в точках співпаде, то математична модель – правильна.
![]() , (17)
, (17)
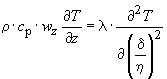 , (18)
, (18)
![]() . (19)
. (19)
Розв'язавши
дану математичну модель (17-19), можна визначити втрату активності при різних
режимах та часі. Це дозволить ще на стадіях проектування обладнання для
отримання БАР підбирати такі технологічні режими та апаратуру (наприклад,
довжину труб апарату), які задовольнять умовам синтезу певних типів БАР, що має
скоротити витрати на їх отримання.