С.Н.Яловенко

Харьковский Национальный Университет Радиоэлектроники

Чёрный предел. Теория относительности. Новый взгляд

Введение

Расширение преобразований лоренца

Рассмотрим две инерциальные системы отсчёта К и К’ (К’ движется относительно К со скоростью v). Направим координатные оси так, как показано на рис.1.

Какому-либо событию в системе К соответствуют значение координат и времени, равные x, y, z, t, в системе К’ – x’, y’, z’. t. В классической физике считалось, что время в обеих системах течёт одинаково, т.е. что t=t’. Если в момент t=t’=0 начала координат обеих систем совпали, то тогда между координатами событий в обеих системах имеются следующие соотношения:

x=x’+vt’=x’+vt

y=y’

z=z’ (1)

t=t’

q=q’ или

В уравнении (1) в ведено расширение на q и назовем это уравнение расширенным преобразованием галилея. Из них вытекает закон сложения скоростей классической механики:

(2)

Легко видеть, что этот закон находится в противоречии с принципом постоянства скорости света. Действительно, если в системе К' световой сигнал распространяется со скоростью с (и'_{х =} с), то согласно (2) в системе К скорость сигнала окажется равной u_x=c+v, т. е. превзойдет C. Отсюда вытекает, что преобразования Галилея должны быть заменены другими формулами. Эти формулы нетрудно найти.

Из однородности пространства следует, что формулы преобразования не должны изменяться при переносе начала координат (т. е. при замене х на х + а и т. д.). Этому условию могут удовлетворять только линейные преобразования. При указанном на рис.1. выборе координатных осей плоскость у =0 совпадает с плоскостью у'=0, а плоскость z=0 - с плоскостью z' = 0. Отсюда следует, что, например, координаты у и у' могут быть связаны только соотношением вида

.

В силу полной равноправности систем К и К' должно также соблюдаться соотношение

с тем же значением , что и в первом случае. Перемножая оба соотношения, получим, что , откуда . Знак плюс соответствует одинаково направленным осям у и у', знак минус — противоположно направленным. Направив оси одинаковым образом; получим:

y=y’ (3)

Такие же рассуждения приводят к формуле:

z=z’ (4)

Обратимся к нахождению преобразований для х и t. Начало координат системы К имеет координату х = 0 в системе К и х' = —vt' в системе К'. Следовательно, при обращении х' + vt' в нуль должна обращаться в нуль и координата х. Для этого линейное преобразование должно иметь вид:

(5)

Аналогично, начало координат системы К' имеет координату х' = 0 в системе К' и х = vt в системе К, откуда следует, что

(6)

Из полного равноправия систем К и К' вытекает, что коэффициент пропорциональности в обоих случаях должен быть один и тот же (различный знак при v в этих формулах обусловлен противоположным направлением движения систем друг относительно друга — если система К' движется относительно К вправо, то система К движется относительно К' влево).

Формула (5) позволяет по известным координатам х' и времени t' события в системе К' определить координату х события в системе K. Чтобы найти формулу для определения времени t события в системе К, исключим х из уравнений (5) и (6) и разрешим получившееся выражение относительно t В результате получим:

(7)

Для нахождения коэффициента пропорциональности используем принцип постоянства скорости света. Предположим, что в момент времени t = t'= 0 (в обеих системах время отсчитывается от момента, когда их начала координат совпадают) в направлении оси х посылается импульс. Именно в этом месте рассуждений вводим расширение представляя свет не как волну, а как частицу обладающей импульсом и массой – виртуальной, но подверженной гравитационному воздействию, так же как и любая материальная частица с массой , где масса находится из уравнений энергии как

E=ħν

И энергию, которую нужна затратить на преодоление гравитации этой массе m равна

То есть световой поток можно представить (упрощенно) как обмен мячиками массой m.

И так световой импульс, производит вспышку света на экране, находящемся в точке с координатой х=а. Это событие (вспышка) описывается координатами х = а, t = b в системе К и х' =а', t’ =b' в системе К', причем а = сb, а' = сb', так что координаты события в обеих системах можно представить в виде:

x=cb, t=b и x’=cb’, t’=b’

Подставив эти значения в формулы (5) и (6), получим:

cb=(cb’+vb’)=(c+v)b’ (8)

cb’=(cb - vb)=(c – v)b .

Перейдем от рассмотрения света как волны к рассмотрению света как частицы обладающей массой m .Введём расширение для уравнения (8) рассматривая свет как импульс mv ( или mc) и расширим уравнение (8) переписав его как:

mcb=γ(cb’+vb’)m’=γ(c+v)b’m’ (8.1)

mcb’=γ(cb – vb)m’=γ(c – v)bm’ .

Перемножив оба уравнения, придем к соотношению

Откуда

(9)

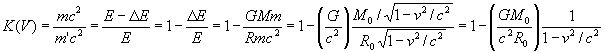Где коэффициент лоренца, коэффициент взаимодействия, - энергия, которую необходимо затратить кванту света на преодоление гравитационных сил. Если то и уравнение (9) приобретает лоренцовский вид, где =L(V).

Подстановка этого значения в (5) и (7) даст окончательные формулы для х и t. Добавив к ним формулы (3) и (4), получим совокупность уравнений;

,

y=y’, (10)

z=z’

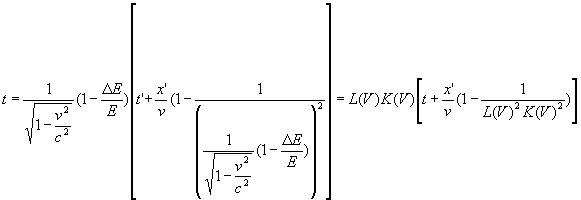
По формулам (10) осуществляется переход от координат и времени, отсчитанных в системе К', к координатам и времени в системе К (короче, переход от системы К' к системе К). Если разрешить уравнения (10) относительно штрихованных величин, получатся формулы преобразования для перехода от системы К к системе K':

,

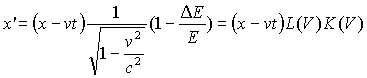y’=y, (11)

z’=z,

Как и следовало ожидать, учитывая полную равноправность систем К и К', формулы (11) отличаются от формул (10) только знаком при v. Формулы (10) и (11) носят название р а с ш ы р е н ы х преобразований лоренца с учётом коэффициента взаимодействия K(V). Легко видеть, что в случае () преобразования переходят в преобразования лоренца, а при преобразования лоренца переходят в преобразования Галилея (1). Таким образом, преобразования Галилея сохраняют значение для скоростей, малых по сравнению со скоростью света. При v>c выражения (10) и (11) для х, t, х' и t' становятся мнимыми. Это находится в соответствии с тем, что движение со скоростью, большей скорости света в пустоте, невозможно. Нельзя даже пользоваться системой отсчета, движущейся со скоростью с, так как при v = с в знаменателях формул для х и t получается нуль.

Основа теории относительность являются лоренцевы преобразования дальше все выкладки аналогичны с заменой на . Дальше (в разделе теория холодного синтеза) будет показана не законченность теории и необходимость введения третьего расширения преобразований Галилея( или третьего отрицания…. +,0, ?)

.

Следствия из р а с ш и р е н и я преобразований Лоренца

Из расширенного преобразований Лоренца вытекает ряд необычных с точки зрения классической механики следствий.

Одновременность событий в разных системах отсчета.

Пусть в системе К в точках с координатами и х₂ происходят одновременно два события в момент времени t_l = t₂ = b. Согласно формулам (11) в системе К' этим событиям будут соответствовать координаты

,

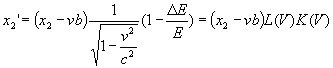
и моменты времени

Из написанных формул видно, что в случае, если события в системе К происходят в одном и том же месте пространства (), то они будут, совпадать в пространстве () и во времени () также и в системе К'. Если же события в системе К пространственно разобщены (), то в системе К' они также окажутся пространственно разобщенными (), но не будут одновременными (). Знак разности определяется знаком выражения ; следовательно, в разных системах К' (при разных v) разность будет различна по величине и может отличаться по знаку. Это означает, что в одних системах событие 1 будет предшествовать событию 2, в других системах, наоборот, событие 2 будет предшествовать событию 1. Заметим, что сказанное относится лишь к событиям, между которыми отсутствует причинная связь.

Длина тел в разных системах. Рассмотрим стержень, расположенный вдоль оси х и покоящийся относительно системы отсчета К' (рис.2).

Длина его в этой системе равна где x\ и х'₂ — не изменяющиеся со временем координаты концов стержня. Относительно системы К стержень движется со скоростью v. Для определения его длины в этой системе нужно отметить координаты концов стержня и х₂ в один и тот же момент времени =t₂=b. Их разность даст длину стержня, измеренную в системе К. Чтобы найти соотношение между и , следует взять ту из формул расширенных преобразований Лоренца, которая содержит х', х и t, т. е. первую из формул (11). Согласно этой формуле

,

Откуда

Или окончательно

(12)

Таким образом, мы получили расширенное лоренцево преобразование для длины стержня

Если стержень длины покоится относительно системы К, то для определения его длины в системе. К' нужно отметить координаты концов и х'₂ в один и тот же момент времени = t'₂ = b. Разность даст длину стержня в системе , относительно которой он движется со скоростью v. Использовав первое из уравнений (10), снова придем к соотношению (12).

Заметим, что в направлении осей у и z размеры стержня одинаковы во всех системах отсчета.

Длительность событий в разных системах. Пусть в точке, неподвижной относительно системы К', происходит событие, длящееся время . Началу события соответствует в этой системе координата и момент времени , концу события — координата х'₂ = а и момент времени Относительно системы К точка, в которой происходит событие, перемещается. Согласно формулам (10) началу и концу события соответствуют в системе :

,

откуда

Введя обозначения , получим:

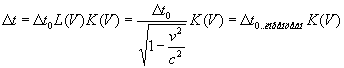(13)

Таким образом, мы получили расширенное лоренцево преобразование для времени.

В этой формуле - длительность события, измеренная по часам системы, движущейся с той же скоростью, что и тело, в котором происходит процесс (тело в этой системе покоится). Иначе "можно сказать, что определено по часам, движущимся вместе с телом. Промежуток измерен по часам системы, относительно которой тело движется со скоростью v.

Время (как будет показано ниже) напрямую связано с массой, поэтому используя инвариант запишем расширенное лоренцево преобразование для массы

(14)

Эффект доплера. Свяжем с приемником света начало координат системы К, а с источником — начало координат системы К' (рис.3).

Оси х и х' направим, как обычно, вдоль вектора скорости v, с которой система К' (т. е. источник) движется относительно системы К, (т. е. приемника). Уравнение плоской световой волны, испускаемой источником по направлению к приемнику, будет в системе К' иметь вид.

(15)

где — частота волны, фиксируемая в системе отсчета, связанной с источником, т. е. частота, с которой колеблется источник. Чтобы не ограничивать общности, мы допускаем, что начальная фаза может быть отлична от нуля. Мы снабдили штрихами все величины, кроме с , которая одинакова во всех системах отсчета.

Согласно принципу относительности законы природы имеют одинаковый вид во всех инерциальных системах отсчета. Следовательно, в системе К волна (15) описывается уравнением:

(16)

где — частота, фиксируемая в системе отсчета К, т. е. частота, воспринимаемая приемником.

Уравнение волны в системе К можно получить из уравнения (15), перейдя от х' и к х и t с помощью расширенных преобразований Лоренца, Заменив в (15) х' и t’ согласно (11), получим:

=

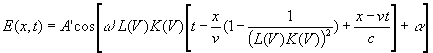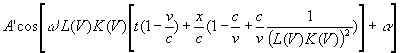= (17)

Из уравнения (17) видно, что при и частота в системе и в системе источника связаны как;

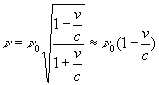(18)

В области значений и частота в системе и в системе источника связаны как:

(18,1)

Другие формулы выводятся аналогично

Сложение скоростей. Рассмотрим движение материальной точки. В системе К положение точки определяется в каждый момент времени t координатами х, у,z. Выражения:

представляют собой проекции на оси х, у, z вектора скорости точки относительно системы К. В системе К' положение точки характеризуется каждый момент времени координатами х’, у', z'. Проекции на оси х’, у', z' вектора скорости точки относительно системы К' определяются выражениями:

Из формулы (10) вытекает, что

Разделим первые три равенства на четвертое, получим формулы преобразования скоростей при переходе от одной системы отсчёта к другой:

(19)

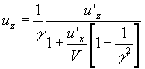
В случае, когда то и уравнение (19) приобретает лоренцовский вид, где 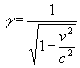=L(V), когда V<<C, соотношение (19) переходят в формулы сложения скоростей классической механики.

Если тело движется параллельно оси х, его скорость и относительно системы К, совпадает с и_х, а скорость и' относительно системы К' — с и'_х. В этом случае закон сложения скоростей имеет вид:

(20)

На рис.4 показано поведение функции , на рис.5 поведение функции

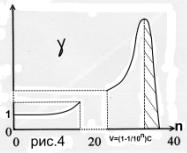
Из рисунков видно , что при достижении скорость падает и меняет знак на противоположный , что означает сопротивление дальнейшему нарастанию скорости в нашем представлении за счёт увеличения линейного размера тела.

Обобщим полученные формулы

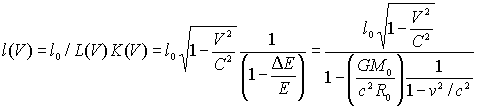
Из формул видно, что, ограничив скорость света, мы получили бесконечную массу. Введя ограничение на массу, ограничив массу черной дырой, т.е. ни одно тело при не может превзойти массу чёрной дыры, к которой оно стремится: .

В результате получили новые бесконечные величины по длине и относительность заряда тела .

Зададимся вопросом:, а есть ли ограничения по длине? Вероятно, да, и эти ограничения связаны с размерами нашей Вселенной, т.е. стремится не к бесконечности, а к ( R ) – радиусу Вселенной, начиная с момента большого взрыва как минимум. В этом смысле длина и время есть проявление одной сущности. Следовательно, при записи

Рассмотрим это влияние в дальнейших частях. Предположительно – это функция дальнодействия и её можно записать как

.

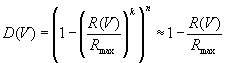Построим обобщающие графики

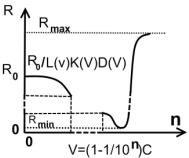
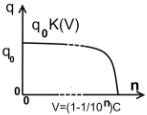
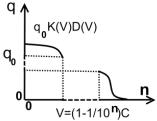
Где L(V)- преобразование лоренца (первое расширение преобразований галилея), K(V) – коэффициент взаимодействия (второе расширение преобразований галилея), D(V) – коэффициент дальнодействия (трете расширение преобразований галилея).

Список используемой литературы

1. А. Эйнштейн. Теория относительности. 2000 Научно-издательский центр. Регулярная и хаотическая динамика

2. Фейнман Р., Лейтон Р., Сэндс М. - Фейнмановские лекции по физике.

3. Принцип относительности” Лоренц, Пуанкаре, Эйнштейн и Минковский; ОНТИ ; 1935 г., стр. 134,51,192

4. Полное собрание трудов, Л. И. Мандельштам; Том 5, стр. 172

5. "Физика пространства-времени"; Э. Ф. Тейлор; Москва., 1963 г.

6. "Общая теория относительности"; Н. В. Мицкевич; Москва., 1927 г.

7."«Чёрный предел. Теория относительности: новый взгляд» ТОВ издательство «Форт» 2009г. ISBN 978-966-8599-51-4

8. Вестнике Национального технического университета «ХПИ» тематический выпуск «Новые решения в современных технологиях» г.Харьков №43 за 2008 год стр.144 С.Н.Яловенко «Чёрный предел.Часть1.Теория относительности. Новый взгляд»