УДК 004.383:656.056

Алдибекова К.А., магистр технических наук

Преподаватель лицея при КазГАСА

Обнаружение особых точек в SURF основано на вычислении детерминанта матрицы Гессе (гессиана).

В данной статье рассматривается научная новизна, выявляющая проблемы и обоснование условий формирования структуры системы распознования образов методом SURF.

Бұл мақалада SURF әдісі арқылы бейнені тану жүйесінің құрылымын қалыптастыру шарттарының проблемалары және негіздеуін анықтауға мүмкіндік беретін ғылыми жаңалық қаралады.

This article describes the scientific novelty, identify problems and justification of the conditions of formation of structure of the system recognizers images by SURF.

Данная система распознавания образов успешно внедрена в такие крупные компании как «Mercedes-Benz», «Volvo», «Subaru» и др., они используют данную систему для распознавания пешеходов. Применение данной системы позволяет на 15% сократить смертность пешеходов и на 30% снизить риск получения ими серьезных травм.

Метод SURF (Speeded Up Robust Features) предназначен для поиска пешеходов в видеопотоке. Данный метод может быть использован в различных отраслях, но по большей части она используется для увеличения безопасности на дорогах, так как пешеходы являются самыми уязвимыми участниками дорожного движения.

Значение гессиана используется для нахождения локального минимума или максимума яркости изображения. В этих точках значение гессиана достигает экстремума.

Матрица Гессе для двумерной функции и ее детерминант определяется следующим образом:

, .

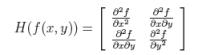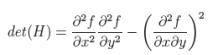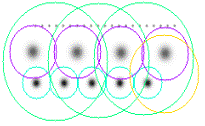На рисунке 1 видно, что особые точки (очерченные цветными кругами) представляют собой локальные экстремумы яркости изображения. Мелкие точки не распознаны как особые, из-за порогового отсечения по величине гессиана.

Рисунок 1 – Локальные экстремумы яркости изображения

На рисунке 2 показаны концы отрезка, распознанные как ключевые точки, с помощью матрицы Гессе.

Теоретически, вычисление матрицы Гессе сводится к нахождению Лапласиана Гауссиан. По сути, элементы матрицы Гессе вычисляются как свертка (сумма произведений) пикселов изображения на фильтры.

Рисунок 2 – Концы отрезка распознанные как ключевые точки

На рисунке 3 изображены дискретизированные фильтры для нахождения четырех элементов матрицы Гессе.

Рисунок 3 - Дискретизированные фильтры для нахождения четырех элементов матрицы Гессе

Однако SURF не использует лапласиан гауссианы в том виде, который изображен на рисунке. Во-первых, по утверждению авторов, дискретизированный лапласиан гауссианы имеет довольно большой разброс значения детерминанта, при вращении образца (напомним, что в идеале гессиан должен быть инвариантен к вращению). Особенно детерминант «проседает» в районе поворота на 45 граудсов. А во-вторых, и это главное, фильтр для лапласиана гауссианы имеет непрерывный характер. Поэтому SURF использует бинаризированную аппроксимацию лапласиана гауссиан.

На рисунке 4 изображены фильтры, используемые для нахождения матрицы Гессе в SURF. Белые области соответствуют значению +1, черные -2 (на третьем фильтре -1), серые – нулевые. Пространственный масштаб – 9x9 пикселов.

Рисунок 4 – Фильтры для нахождения матрицы Гессе в SURF

Этот фильтр более устойчив к вращению, и его можно эффективно вычислить с помощью интегральной матрицы.

Таким образом, в SURF, гессиан вычисляется так:

det(H_approx) = D_xx D_yy – (0.9D_xy)²,

где, Dxx, Dyy, Dxy – свертки по фильтрам, изображенным на рисунке вверху.

Коэффициент 0.9 имеет теоретическое обоснование, и корректирует приближенный характер вычислений. В методе задается пороговое значение гессиана. Если вычисленное значение для пиксела выше порога – пиксел рассматривается как кандидат на ключевую точку.

Для одного и того же пиксела, гессиан может меняться при изменении масштаба фильтра. Решение этой проблемы только одно – перебирать различные масштабы фильтров и поочередно их применять к данному пикселу.

Рисунок 5 - Первые три октавы метода SURF

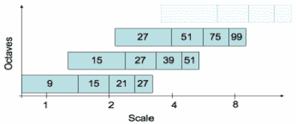На рисунке 5 показаны первые три октавы метода SURF. Цифры в прямоугольниках показывают размер фильтра Fast-Hessian. Логарифмическая шкала снизу – показывает масштабы, покрываемые октавами. Шаг размера фильтра в первой октаве – составляет 6, во второй – 12, в третьей – 24 и так далее. Как видим, октавы значительно перекрываются друг другом. Это увеличивает надежность нахождения локальных максимумов.

Заключение

Методы распознавания образов позволяют решать задачи классификации, прогноза и управления процессами и сложными системами, а также принятия в заданных условиях наиболее рациональных решений, основанных на опыте прошлого. Несмотря на большое разнообразие методов и подходов к распознаванию образов, в настоящее время не существует единого универсального алгоритма, позволяющего решить задачу классификации объектов. Среди возможностей системы должны быть: распознавание пешеходов, простота работы с видеофайлами.

Список использованной литературы

1. Журавлев Ю.И. Об алгебраическом подходе к решению задач распознавания или классификации // Проблемы кибернетики. М.: Наука, 2005. - Вып. 33. С. 5-68

2. Потапов А.С. Распознавание образов и машинное восприятие. - С-Пб.: Политехника, 2007. - 548 с

3. Ryuji Funayama, Hiromichi Yanagihara, Luc Van Gool, Tinne Tuytelaars, Herbert Bay, "ROBUST INTEREST POINT DETECTOR AND DESCRIPTOR", published 2009-09-24

4. N. Dalal and B. Triggs. Histograms of oriented gradients for human detection // Conference on Computer Vision and Pattern Recognition (CVPR), 2005.

5. D. Geronimo, A.M. Lopez, A.D. Sappa, and T. Graf. Survey of pedestrian detection for advanced driver assistance systems // Pattern Analysis and Machine Intelligence, 2010.

6. «Теория распознавания образов (статистические проблемы обучения)», В. Н. Вапник, А. Я. Червоненкис. Издательство «Наука», Главная редакция физико-математической литературы, М., 1974, 416 стр.