DEVELOPMENT AND OPERATION OF HYDROTRANSPORT
SYSTEMS UNDER SEVERE ENVIRONMENTAL CONDITIONS
S.Yu.Avksentiev,A.K. Nikolaev, V.P. Dokoukin
St. Petersburg State Mining Institute
St. Petersburg, Russia
The energy crisis which becomes more
evident in Russia stems in many respects from unjustified high consumption of
energy resources. Development and exploitation of principal oil and gas
deposits located in remote areas with severe climatic conditions require
considerable investments increasing essentially the cost of power generation.
Account should be taken also of the fact that oil and gas resources are
nonrenewable. An alternative fuel for heat and power generation is coal the
reserves of which in Russia are quite substantial. For this reason the coal
extraction by 2020 will amount to 450-550 million tons. The use of coal, as a
solid fuel for heat power plants and heating plants, is complicated by its
transportation from extraction to processing and consumption sites.
Remoteness of the principal coal
mining areas (Kuzbass, Kansk-Achinsk field, Vorkuta) from the main centers of
its consumption in the European part of the country, Siberia and Far East makes
urgent the problem of coal transportation. Of all possible transportation
methods (railway, conveyor, pipeline) the most efficient is hydrotransport
which provides continuous transportation at comparatively low capital and
working costs, as confirmed by construction and operation of extended coal
pipelines in many countries.
In the USA twelve coal pipelines
with an overall length of about 20,000 km and a total throughput capacity of
263 million tons per year have been designed. The pipeline diameters vary from
560 to 1220 mm [1]. The coal pipelines traverse different climatic zones and
high-seismicity zones.
In Canada the coal pipeline 1287 km
in extent has been designed to connect five new coal mines with west ports. Its
throughput capacity will amount to 10.2 million tons of coal per year.
Despite the fall in prices for
nonferrous metals many countries continue to build new large-scale and to
reconstruct operating mining enterprises, where the pipeline transport is
widely used for transportation of ore processing products.
The world’s largest copper deposit
Collahuasi in Chile is located at an altitude of 4500 m above sea-level in the
Andes. As estimated, the prospective enterprise will produce up to 900,000 tons
of copper concentrate per year to be transported to a port through the pulp
pipeline 180 mm in diameter and 207 km in length. The pulp pumping station
located at an elevation of 4300 mm pumps the pulp to a mountain pass to an
altitude of 4800 mm, from whence the concentrate is delivered by gravity to a
discharge port. This variant was considered along with the road and railroad
transport and was chosen as the most cost-effective and environmentally safe.
The enterprise will run at an unprecedented altitude above sea-level.
In Russia the pipelines for
transportation of solid mineral products were not more than 10-20 km in extent,
and only at the end of 80-ies the Belovo-Novosibirsk pilot coal pipeline 264 km
in length with a throughput capacity of 3 million tons per year was built for
transportation of coal-water pulp. The pipeline, as compared with railroad
transport, allows the current and capital costs to be reduced by a factor of
1.5.
Intensive development of Siberian
and Far North regions makes necessary investigation of the problems related to
transportation of water, different mixtures and pulps under severe climatic
conditions. Operation of water pipelines laid in eternally frozen ground [3,4],
hydroplant pipelines [5], hydraulic mining pipelines transporting water-sand
mixtures [6] is fraught with hazard of inner icing of pipes both with liquid
moving through pipes and during downtime, which results in an increase in
hydrodynamic resistance. Significant contribution to ice-thermal calculation of
pipelines was made by Russian scientists and engineers (P.A. Bogoslovsky, A.M.
Estifeev, D.N. Bibikov, Yu.A. Popov, V.M. Zhidkikh, N.N. Zenger, A.V. Lyutov,
et al.).
Many researchers noted that it is
not always necessary to strive to completely eliminate icing, since costs of
heating, thermal insulation of tubes and earth works are unjustifiably high
(N.N. Zenger, V.P. Stegantsev, S.V. Khizhnyakov et al.).
The study of the ice regime of
pipelines as applied for hydropower plants showed that their inner icing, when
in operation, is possible (P.A. Bogoslovsky). The fundamental difference in
operation between pipelines in a system with centrifugal pumps and water
pipelines of hydropower plants consists in the availabilty of feedback (pump «pipeline). Pumps at a specified flow rate
develops the head necessary to overcome the forces of hydraulic resistance.
Yu.A. Popov investigated the ice regimes of hydraulic mining pipelines with
complicated production engineering applied and under time-varying weather
conditions. On this basis he developed the fundamentals of the theory of
water-sand mixture transportation under severe climatic conditions for
hydraulic mining. The method of ice-thermal calculation of water pipeline
system providing for alternate operation and idle of the hydraulic system is
developed in study [7].
To prevent failures caused by
freezing of transported liquids it is necessary to envisage at the design
stage, when calculating ice-thermal regimes of such pipeline systems, possible
unfavorable operation conditions connected with changes of weather conditions,
possible shutdowns, to calculate the thickness of thermal insulation, to
consider several design versions to determine the optimal one.
When designing large-extent transport facilities new problems arise and novel calculation methods should be elaborated, such as:
n establishment of relation between
the hydrodynamic and thermal regimes in pipelines of hydrotransport systems;
n the effect of unsteady processes on
the system performance reliability during start-up and shutdown;
n definition of mutual effect of the
system «environment ® (pump « pipelines)»;
n elaboration of the method for
installation of pipelines and devices compensating for temperature
deformations.
The urgency of these problems has
determined the line of scientific activities undertaken at the Saint Petersburg
Mining Institute (Technical University).
At the first stage the theoretical
and experimental works were carried out to investigate the effect of solid
phase distribution over the pulp-carrying flow section on the intensity of heat
transfer from flow to pipeline wall.
The presence of solid particles in
the liquid-carrying flow complicates essentially the process of heat exchange
with the pipe wall. For the hydrodynamically developed flow it is possible to
consider non-Newtonian hydromixture as a dummy liquid with an increased
density, since solid particles move with a local velocity of liquid [9]. Such a
model makes it possible to use in the thermal calculation the averaged
characteristic lÏ - the thermal conductivity of
hydromixture in the radial direction [8]. The hydrodynamical axis of the flow
is found to be displaced upwards, because large particles move in the
near-bottom zone. The axial velocity of hydromixture wx will
depend on the angle j which is measured in the plane
perpendicular to the pipe geometrical axis from the vertical and varies in the
range from 0 to p (Fig.1).
Processing of the velocity profiles
of pulp-carrying flows of different concentrations [9] makes it possible to
take the functional dependence wx(j) as cos(j/m), where m is the
experimentally defined constant. As estimated, m»3. In this case the velocity profile
in the pulp-carrying flow can be taken as:
![]() wx(j) = 2 wav(1-R2)cos
wx(j) = 2 wav(1-R2)cos![]() , (1)
, (1)
where wav - average velocity of hydromixture motion,
m/s; R=r/r0 - reduced pipe radius; r0 - pipe radius, m.
The heat exchange equation for the pulp flow in a pipe is of the form:
![]() , (2)
, (2)
where t - pulp temperature, K; a
=lÏ/(cr)Ï; (cr)Ï - volumetric heat capacity of pulp,
J/(m3.K); x- the coordinate characterizing the pipe length, m.
Let us choose, as a characteristics value, the
wall temperature tc, treating it further as a constant. If t0 is
the pulp constant temperature at the pipeline input, then by introducing the
dimensionless variables:
![]()
![]() ,
,
Eq.(2) can be of the form:
![]() . (3)
. (3)
The boundary conditions are of the form:
a) on the pipe surface the temperature is specified as:
q = 0 at R=1 (4)
b) at the input cross-section (x=0) the temperature is constant:
q=1 at X=1. (5)
To estimate the temperature regime
[10] let us choose the approximate method for solution of the boundary problem
(3)-(5) based on the transformation of convolution of the functions f1*f2
[11]:
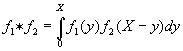 (6)
(6)
Differential equation (3) written with the convolution transformation is
of the form:
![]() , (7)
, (7)
where Ñ2 - Laplace operator.
Eq. (7) is used to form the functional of the heat exchange process
[11]:
![]() (8)
(8)
The integration domain D
covers the pipeline cross-section. The identity of this functional to Eq.(3)
with conditions (4) and (5) is established by taking the first variation with
respect to q.
The approximate solution is found in the form of the function
combination:
![]() , (9)
, (9)
where k - the approximation number.
As is known from the theory of
approximate solutions [12], the first approximation yields the predicted error
not exceeding 10%, but with an appropriate choice of the approximating
functions ji the error can be even less.
The first approximation is found in the form:
![]() (10)
(10)
It is seen that the coordinate function j1 satisfies identically the boundary condition
in Eq.(5).
By substituting q1 into functional (8) and integrating with
respect to the pipeline cross-section we obtain the numerical value of the
coefficients:
![]() (11)
(11)
By varying expression (11) with respect to the argument g we get:
![]() .
.
As dg¹0, the extremality of functional
(11) requires that
![]() (12)
(12)
The equivalent form of the differential equation is obtained by taking a derivative with respect to X:
![]() , (13)
, (13)
with the boundary condition taking the form:
g(0) =1.709 (14)
By separating the variables in Eq.(13), integrating and using condition
(14) we get:
g=1.709exp(-18.5X) (15)
Finally, the first approximation for temperature is as follows:
![]() (16)
(16)
The results of the calculation made by Eq.(16) are tabulated. The average temperature of the pulp-carrying flow is calculated to analyze the error caused by the approximate method used.
Table 1. Dimensionless temperature q as a function of X, j, R.
|
X |
j |
q |
||||
|
|
|
R=0.1 |
R=0.3 |
R=0.5 |
R=0.7 |
R=0.9 |
|
|
p/6 |
0.810 |
0.745 |
0.614 |
0.417 |
0.156 |
|
|
p/3 |
0.773 |
0.711 |
0.586 |
0.398 |
0.148 |
|
0.01 |
p/2 |
0.712 |
0.655 |
0.540 |
0.367 |
0.137 |
|
|
2p/3 |
0.630 |
0.579 |
0.477 |
0.325 |
0.121 |
|
|
5p/6 |
0.529 |
0.486 |
0.400 |
0.272 |
0.101 |
|
|
p |
0.411 |
0.378 |
0.312 |
0.212 |
0.079 |
|
|
p/6 |
0.387 |
0.355 |
0.293 |
0.199 |
0.074 |
|
|
p/3 |
0.369 |
0.339 |
0.279 |
0.190 |
0.071 |
|
0.05 |
p/2 |
0.340 |
0.312 |
0.258 |
0.175 |
0.065 |
|
|
2p/3 |
0.301 |
0.276 |
0.228 |
0.155 |
0.058 |
|
|
5p/6 |
0.252 |
0.232 |
0.191 |
0.130 |
0.048 |
|
|
p |
0.196 |
0.180 |
0.149 |
0.101 |
0.038 |
|
|
p/6 |
0.153 |
0.141 |
0.116 |
0.079 |
0.029 |
|
|
p/3 |
0.146 |
0.134 |
0.111 |
0.075 |
0.028 |
|
0.10 |
p/2 |
0.135 |
0.124 |
0.102 |
0.069 |
0.026 |
|
|
2p/3 5p/6 |
0.119 0.100 |
0.110 0.092 |
0.090 0.076 |
0.061 0.051 |
0.023 0.019 |
|
|
p |
0.078 |
0.072 |
0.069 |
0.040 |
0.015 |
 (17)
(17)
The estimation of approximation at the input cross-section can be obtained by comparing the boundary condition at the input (5) and the value of Eq.(17) at X=0:
qav = 0.9479 @ 0.95
It is seen that the approximate solution yields an error of ~5%.
The pulp temperature can be estimated by Eqs.(16) and (17) with an accuracy sufficient for the engineering calculations.
The aim of the experimental investigations was to obtain the dependence for calculation of the heat transfer coefficient when the pulp flows through the pipeline.
The results of the experiments with
water comply with the dependence given by M. Mikheev in [12]:
Nu =0.026Re0.8Pr0.4
In this case the error did not exceed ±7%.
The experimental data on heat exchange between the pulp and the pipe wall were processed in compliance with the obtained criteria dependence:
 ,
,
where Rep - Reynolds
number of pulp; Prp - Prandtl number of pulp; C1 - liquid
heat capacity; C2 - heat capacity of solid particles; l1 - thermal conductivity of liquid; l2 - thermal conductivity of solid particles; l3 - thermal conductivity of pulp.
The obtained formula is recommended for thermal calculations of the pipelines intended for transportation of the non-Newtonian pulp.
References
1.
15th
Biennial Low Ranks Fuels Symposium, Minnesota, 22-25 May, 1989.
2.
Yu.N.
Malyshev, K.N. Trubetskoy, Coal Industry of Russia at the threshold of the XXI
Century (reported at XVIII Mining Congress).
3.
N.N.
Zenger, Peculiar features of water pipelines in permafrost conditions, L.
Stroyizdat, 1964 (in Russian).
4.
N.Z.
Gusev et al., Thermal calculations of water pipelines laid in frozen ground,
Irkutsk Polytechnical Institute, Irkutsk, 1971 (in Russian).
5.
P.A.
Bogoslovsky, Ice operation regime of hydraulic power plant pipelines,
Gosenergoizdat, 1950 (in Russian).
6.
Yu.A.
Popov, Some problems of hydraulic and thermal calculation of pipelines during
transportation of water and water-sand mixtures in winter (Thesis for a
candidate’s degree), Novosibirsk, 1969 (in Russian).
7.
Yu.A.
Popov, E.N. Guselnikov, Calculation of complicated types of icing of pipelines,
Izvestiya Vuzov, Stroitelstvo, No.11, 1995 (in Russian).
8.
Z.P.
Gorbis, Heat exchange and hydromechanics of disperse through flows, M.,
Energiya, 1972.
9.
N.A,
Silin, Hydrotransport, Kiev, Naukova Dumka, 1974 (in Russian).
10. V.A. Romanov, Engineering methods for
calculation of subsurface water filtration, L., published by LGI, 1979 (in
Russian).
11. N.N Tao, Theory. Physics, v.51, 1965.
12. M.A. Mikheev, I.M. Mikheeva, The principles of
heat transfer, M., Energiya, 1973 (in Russian).