УДК 517.98

МОДЕЛЬ «ХИЩНИК-ЖЕРТВА» В НЕЛОКАЛЬНОЙ ПОСТАНОВКЕ

Бейбалаев В.Д.

Дагестанский государственный университет

367025, г. Махачкала, ул. Магомеда-Гаджиева 43 «А», e-mail: kaspij_03@mail.ru

Введение

Современные холистические взгляды на естественнонаучную картину мира, включающую физические, биологические и другие процессы, опираются на фундаментальный принцип всеобщей связи природных явлений и на принцип развития. При этом выделяется физическое (биологическое) ядро природных систем как совокупность низших редукционистских форм материи со своими законами движения [1]. Сам принцип подчинения нелинейной динамики в математическом плане основывается на идее разделения исходной системы на медленные и быстрые подсистемы. При этом осуществляется процедура адиабатического исключения переменных с характерными временными масштабами. Помимо принципа подчинения, для нелинейной динамики важное значение имеет также понятие параметра порядка.

Для исследования динамических процессов в физических и биологических системах настоящее время наряду с методами, основанными на обычных дифференциальных уравнениях, применяют и методы, основанные на дифференциальных уравнениях дробного порядка [5-7].

Нелокальная модель «хищник-жертва»

В качестве нелокальной модели «хищник-жертва» исследована система дифференциальных уравнений с производными дробного порядка вида:

(1)

где - производная Caputo [2], -коэффициент убыли хищников, - их численность в данный момент времени, - их численность в начальный момент времени, - коэффициент убыли жертв при встрече с хищником, - коэффициент, зависящий от того, как часто встреча хищника с жертвой заканчивается трапезой, - их численность в начальный момент времени, - параметр, учитывающий информацию о «прошлом» системы.

В системе (1), если взять , то получим модель «хищник-жертва», предложенный в 1931 году Вито Вольтером.

Разложим правые части системы (1) вблизи стационарной точки , и ограничимся случаем малых отклонений от положения равновесия

Тогда система (1) примет вид:

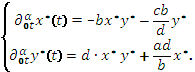
Так как и малы, пренебрежем слагаемым . Тогда

(3)

Пусть – область определения . Тогда для любых функций справедливы равенства:

,

, (4)

где – производная Римана- Лиувилля. Воспользовавшись равенствами (4), систему (3) можно привести к виду:

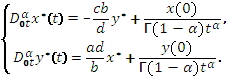(5)

Пусть - решение системы (5), тогда применяя преобразования Лапласа к системе (5), получим:

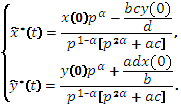(6)

Воспользовавшись равенствами [5,6]:

получим выражения для оригиналов функций

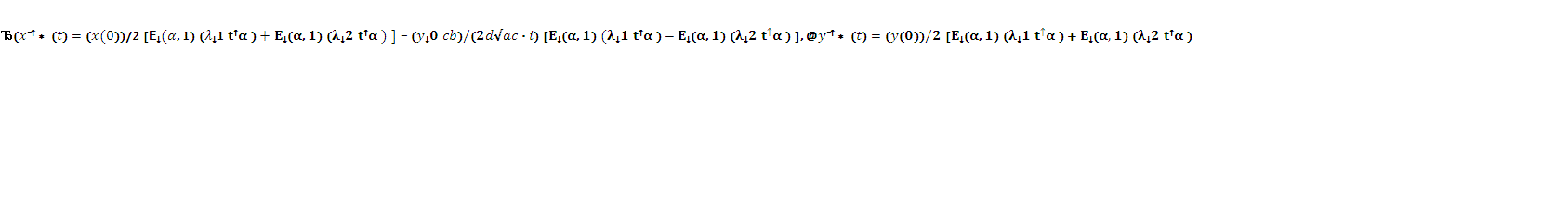(7)

Литература

1. Колесников А.А. Основы синергетики управляемых систем. Уч.-изд. л.-7,7, Таганрогский ГРУ.- 2001.-123с.

2. Самко С.Г., Килбас Ф.Ф., Маричев О.И. Интегралы и производные дробного порядка и некоторые приложения.- Минск: Наука и техника.- 1987.- 688 с.

3. Нахушев А.М. Элементы дробного исчисления и их применение.- Нальчик, 2003.- 299 с.

4. Бейбалаев В.Д. Решение начальной задачи для дифференциального уравнения фрактального осциллятора.// Вестник СамГТУ, серия «Фииз.-мат. науки».-№2(19).-2009.-с.240-242.

5. Назаралив М. А., Мейланов Р.П., Бейбалаев В.Д., Шабанова М.Р. Особенности фазовой траектории фрактального «брюсселятора»// Сб. трудов седьмой Всероссийской научной конференции с международным участием «Математическое моделирование и краевые задачи», Самара.- 2010.- Ч.3.- С.204-210.

6. Назаралиев М.А., Бейбалаев В.Д. Нелинейные колебания в средах с фрактальной структурой // Сб. трудов международного Российско-Болгарского симпозиума «Уравнения смешанного типа и родственные проблемы анализа и информатики», Нальчик-Хабез.- 2010.- С. 177-180.