Математика/Прикладная математика
К. ф.-м. н. Касьянюк В.С.,
Вольчина И.И.
Киевский национальный
университет им. Тараса
Шевченко, Украина
Об
использовании метода кусочно-линейной аппроксимации функциональных зависимостей
по нечетким данным в задаче распознавания запахов
Важными задачами, возникающими в рамках
проблемы распознавания запахов, являются задача определения состава летучего
вещества и количественных характеристик его элементов, а также задача
классификации исследуемых одорантов по предварительно установленным классам
летучих веществ. Во многих случаях задача выяснения состава летучего вещества
рассматривается как подзадача моделирования обонятельной системы.
Для создания "хорошей" газоаналитической
сенсорной системы можно выбрать несколько путей: оптимизация газодинамических
характеристик, использование слоев с лучшими селективными свойствами, совершенствование математического аппарата обработки экспериментальных
данных. Среди традиционных методов, используемых для распознавания газовых
смесей, отметим метод главных компонент (PCA), дискриминантный анализ (DA) и нейронные сети (Neural Network) [1,2]. К сожалению,
эти методы или не дают достаточно надежной
идентификации, или требуют привлечения больших вычислительных мощностей. К
тому же в реальных условиях данные на выходе обонятельных рецепторов искажены
шумами, и для анализа этих данных необходимо максимально уменьшить их влияние. По
мнению авторов, лучшим выходом из этой ситуации является построение газоаналитической
сенсорной системы в рамках концепции "прибор + компьютер = новые
возможности", согласно которой нужный эффект достигается за счет
математической обработки полученных экспериментальных данных. Применение таких
алгоритмов обработки дает ряд преимуществ: эти алгоритмы устойчивы к погрешностям в данных, обеспечивают более
точные результаты, их достаточно легко реализовать на обычных персональных
компьютерах, т.е. нет необходимости вкладывать значительные средства в создание
нового прибора с улучшенными характеристиками. Кроме того, такие алгоритмы не предполагают
большого количества вычислений, т.е. обработку результатов измерений можно
проводить в режиме реального времени.
Математическая постановка задачи заключается в следующем.
Будем считать, что запах представлен вектором концентраций элементарных
одорантов. Результатом измерения прибором некоторого летучего соединения является
определенное количество числовых последовательностей, отражающих изменение во
времени реакций сенсоров на исследуемое вещество; количество
последовательностей равно числу сенсоров. Задача состоит в нахождении вектора
элементарных одорантов, т.е. запаха, по последовательностям реакций сенсоров на
данное вещество. Предложенный в данной работе метод предполагает наличие этапа
обучения, в результате которого известным соединениям (необязательно тем же самым,
что потом подаются для распознавания) ставится в соответствие реакция датчиков на
них.
Для решения поставленной
задачи распознавания запахов будем
использовать метод восстановления функциональных
зависимостей, предложенный в [3]. Речь пойдет о задаче аппроксимации функции y (·) : T® Y, принадлежащей известному классу
функций (в данном случае линейных), по результатам наблюдений значений ее
аргумента (t1, …, tN) и соответствующих значений функции y1, …, yN,
причем данные наблюдений известны неточно.
Будем
предполагать, что количество сенсоров газоаналитической установки (базовых
одорантов) равно l, а концентрация
одоранта является линейной функцией времени. Тогда на выходе прибора, который
измеряет концентрацию некоторого летучего соединения, мы наблюдаем l векторов: ![]() в моменты времени
в моменты времени ![]() .
.
Разобьем полученные данные
по k интервалам группировки:
![]() , причем в каждом интервале имеем
, причем в каждом интервале имеем ![]() наблюдений. Обозначим их
наблюдений. Обозначим их ![]() . Для каждого конкретного интервала выберем следующую линейную
модель связи между y и t:
. Для каждого конкретного интервала выберем следующую линейную
модель связи между y и t:
![]() ;
; ![]()
В отсутствие какой бы то ни
было статистической информации о погрешностях измерений будем считать, что ![]() имеют нечеткие погрешности
имеют нечеткие погрешности ![]() , т.е.:
, т.е.:
![]() ,
,
где ![]() – нечеткий вектор выхода (тогда
– нечеткий вектор выхода (тогда
![]() – наблюдаемые его значения),
– наблюдаемые его значения),
![]() – значения нечеткого вектора
погрешностей, распределение которых определим следующим образом: для
вектора
– значения нечеткого вектора
погрешностей, распределение которых определим следующим образом: для
вектора ![]() функция распределения
имеет вид
функция распределения
имеет вид
 ,
,
где ![]() – непрерывная строго монотонная убывающая функция, причем
– непрерывная строго монотонная убывающая функция, причем
![]() .
.
Значения ![]() определяют, насколько погрешность отклоняется
от нуля. при
определяют, насколько погрешность отклоняется
от нуля. при ![]() ом измерении. Из
построения модели следует, что оценкой погрешности является значение
ом измерении. Из
построения модели следует, что оценкой погрешности является значение
![]() . Следуя теоретико-возможностному подходу, разработанному в
[3], для того, чтобы модель
максимально соответствовала действительности, нужно подобрать такие
. Следуя теоретико-возможностному подходу, разработанному в
[3], для того, чтобы модель
максимально соответствовала действительности, нужно подобрать такие
![]() и
и ![]() , чтобы приведенная выше оценка была
, чтобы приведенная выше оценка была ![]() оптимальной, т.е. минимизировала необходимость ошибки. Поскольку входные
данные можно считать значениями непрерывной функции, то потребуем, чтобы и
аппроксимирующая функция удовлетворяла условию непрерывности:
оптимальной, т.е. минимизировала необходимость ошибки. Поскольку входные
данные можно считать значениями непрерывной функции, то потребуем, чтобы и
аппроксимирующая функция удовлетворяла условию непрерывности: ![]() ,
, ![]() .
.
В качестве характеристической функции для нечеткого
множества ![]() , следуя [3], выберем:
, следуя [3], выберем:
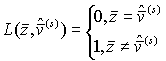 ,
,
где ![]() – вектор всех оценок погрешностей
размерности
– вектор всех оценок погрешностей
размерности ![]() ;
; ![]() .
.
Теперь условие ![]() оптимальности можно
записать в виде:
оптимальности можно
записать в виде:
![]()
![]() ,
, ![]() ,
,
где ![]() (·) – необходимость погрешности.
(·) – необходимость погрешности.
Решив приведенную задачу условной
оптимизации, мы получим оптимальные значения параметров модели.
Учитывая вид ![]() , приходим к
выводу, что
, приходим к
выводу, что ![]() будет достигаться в точках, для которых
будет достигаться в точках, для которых ![]() , т.е.
, т.е. ![]() . После преобразований получаем:
. После преобразований получаем:
![]()
![]() ,
, ![]() ;
;
![]()
![]() ,
, ![]()
Отсюда:

![]() ,
, ![]()
или:
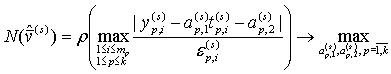
![]() ,
, ![]()
Теперь можно воспользоваться определением функции ![]() :
:

![]() ,
, ![]()
Преобразуем полученную задачу до вида задачи линейного программирования:
![]()
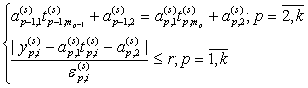
![]()
Для решения этой задачи воспользуемся симплекс-методом (или одной из его
модификаций) и получаем вектор:
![]()
размерности ![]() , который
можно рассматривать как характеристический вектор вещества
, который
можно рассматривать как характеристический вектор вещества ![]() .
.
Приведем пример использования метода
кусочно-линейной аппроксимации для распознавания летучих веществ по их запахам.
Как уже отмечалось выше, первоначально на вход газоаналитической системы
подаются известные вещества и смеси. Для каждого из них находится
вышеупомянутый характеристический вектор, который заносится в базу данных. Для характеристических
векторов введем метрику ρ(A, B)
= sqrt ([A – B, A – B]),
где [.,.] – скалярное произведение, после чего выберем порог близости ![]() , на который накладывается следующее ограничение: если А и В
– характеристики известных веществ, то ρ(А, В)
> 2δ.
, на который накладывается следующее ограничение: если А и В
– характеристики известных веществ, то ρ(А, В)
> 2δ.
Теперь, когда на вход газоаналитической
системы подается неизвестное вещество, вычисляется его характеристика А. Среди всех характеристик, которые есть
в базе данных, находим такую характеристику В,
что ρ(А, В) < δ. Если B
существует, то делаем вывод о том, что исследуемое вещество и вещество,
которому соответствует B, совпадают,
в противном случае считаем, что состав исследуемого вещества существенно отличается
от всех веществ из базы данных.
Рассмотрим применение данного метода на примере
распознавания запаха хлора. В вычислительном эксперименте использовались
данные, полученные с помощью газоаналитической сенсорной системы, разработанной
в Институте физики полупроводников НАН Украины [4,5]. Согласно эксперименту на
вход газоаналитической системы подавался воздух под давлением с высокой
концентрацией хлора. За время ![]() были сделаны замеры с
помощью 8 сенсоров, представленные на Рис. 1.
были сделаны замеры с
помощью 8 сенсоров, представленные на Рис. 1.
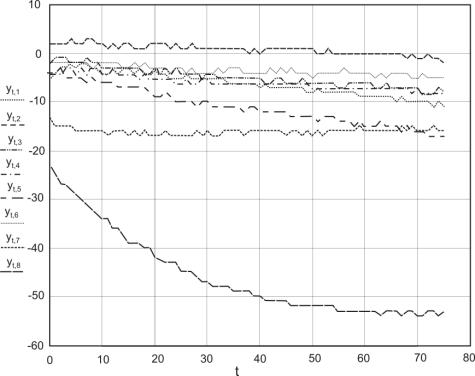
Рис. 1. Данные измерений вещества хлор (первое измерение)
После группировки данных рассматривалось по 12 измерений
для каждого сенсора и решалась каноническая задача линейного программирования
при помощи модифицированного симплекс-метода. Полученное решение - ![]() является характеристикой вещества хлор и
состоит из 192 элементов. Далее проводились обратные действия: по вектору
является характеристикой вещества хлор и
состоит из 192 элементов. Далее проводились обратные действия: по вектору ![]() строилась аппроксиманта результатов измерения
(см. Рис. 2). На Рис. 3-5 приведены результаты сравнения реальных и
промоделированных данных
строилась аппроксиманта результатов измерения
(см. Рис. 2). На Рис. 3-5 приведены результаты сравнения реальных и
промоделированных данных ![]() для
для ![]() ,
т.е. по 2-му, 5-му и 8-му сенсорам соответственно.
,
т.е. по 2-му, 5-му и 8-му сенсорам соответственно.

Рис. 2. Аппроксимация измерений хлора
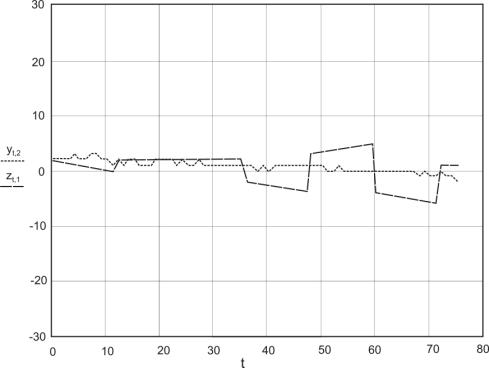
Рис. 3. Аппроксимация
данных по 2-му сенсору

Рис. 4. Аппроксимация данных по 5-му сенсору
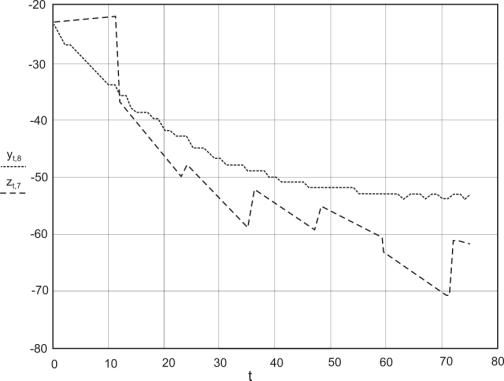
Рис. 5. Аппроксимация
данных по 8-му сенсору
На рисунках видно, что промоделированные данные в незначительной
степени отклоняются от измеряемых.
Модель можно улучшить путем уменьшения
интервалов группировки и уменьшения ![]() для каждого сенсора
соответственно, а также путем удаления некоторых интервалов времени, на которых
результаты измерений вызывают сомнения. Обычно такие решения принимает ЛПР
(лицо, принимающее решение), человек, который хорошо ориентируется в физике
процесса и может учесть различные факторы и условия измерения.
для каждого сенсора
соответственно, а также путем удаления некоторых интервалов времени, на которых
результаты измерений вызывают сомнения. Обычно такие решения принимает ЛПР
(лицо, принимающее решение), человек, который хорошо ориентируется в физике
процесса и может учесть различные факторы и условия измерения.
Рассмотрим теперь задачу распознавания двух
веществ. Вновь проведем измерения вещества хлор и на выходе газоаналитической
системы получим другие экспериментальные данные (См. Рис. 6). Эти данные
несущественно отличаются от данных, представленных на Рис. 1. Ожидаемая модель
также должна несущественно отличаться от предыдущей.
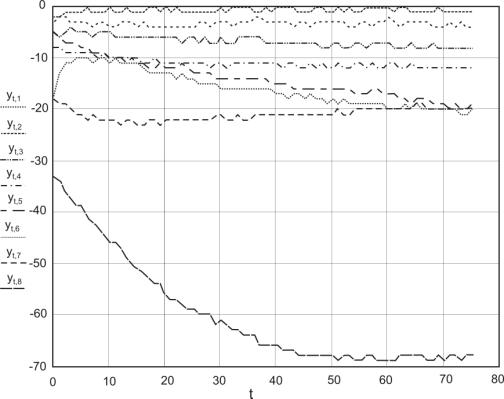
Рис. 6. Данные по
измерению вещества хлор (второе измерение)
Построим вектор
![]() по второму измерению
хлора и найдем отклонение одного измерения от другого по их характеристическим
векторам
по второму измерению
хлора и найдем отклонение одного измерения от другого по их характеристическим
векторам ![]() и
и ![]() :
: ![]() = 93.833.
= 93.833.
Теперь подадим на вход газоаналитической
системы вещество из другого класса, которое существенно отличается от хлора, например,
коньяк. Результаты измерений изображены на Рис. 7.
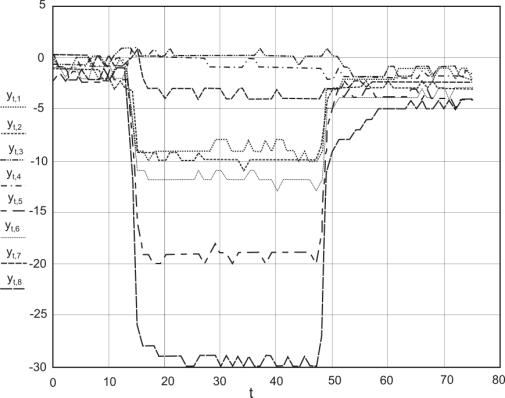
Рис. 7. Данные по
измерению вещества коньяк
После построения вектора ![]() по
измерениям коньяка найдем отклонение
по
измерениям коньяка найдем отклонение ![]() от
от ![]() :
: ![]() = 290.927. Видно, что отличие характеристик хлора и коньяка
намного больше, чем отличие характеристик
различных измерений хлора, т.е. при небольшом d хлор и коньяк будут различаться алгоритмом, что и подтверждает
эффективность его использования.
= 290.927. Видно, что отличие характеристик хлора и коньяка
намного больше, чем отличие характеристик
различных измерений хлора, т.е. при небольшом d хлор и коньяк будут различаться алгоритмом, что и подтверждает
эффективность его использования.
Заметим, что распознавание коньяка было выбрано только для
примера. Аналогичным образом можно распознавать другие одоранты или смеси
одорантов, распределять одоранты по классам, естественно, после соответствующих
измерений, а при определенных условиях можно распознавать и летучие соединения,
предварительно проведя этап обучения на компонентах этих соединений.
Таким образом, предложенный в работе метод
кусочно-линейной аппроксимации по нечетким данным позволяет проводить распознавание
запахов независимо от конкретных сенсорных систем. Это становится возможным благодаря
наличию этапа обучения, в ходе которого используется информация только о
результатах тестовых измерений без учета сложной внутренней структуры самой газоаналитической
сенсорной системы – поставщика данных. Также преимуществом данного метода
является тот факт, что с самого начала метод предполагает наличие ошибок в
данных, причем концептуально распознавание ориентировано на минимизацию
необходимости ошибок.
Предложенный в работе метод достаточно прост
в реализации и позволяет проводить распознавание в реальном масштабе времени.
Таким образом, использование данного метода в совокупности с оптимально
выбранными чувствительными покрытиями сенсоров может значительно улучшить
процесс распознавания летучих соединений и молекул газоаналитическими
системами.
Литература:
1. Zieger Ch. et al. Bioelectronic noses: a
status report. Part II // Biosensors & Bioelectronics.
– 1998. – №13. – P. 539-571.
2. Jurs P.C., Bakken G.A., McClelland H.E. Computational
Methods for the Analysis of Chemical Sensor Array Data from Volatile Analytes
// Chemical Reviews. – 2000. – Vol. 100,
– P. 2649-2678.
3.
Пытьев
Ю.П. Возможность. Элементы теории и применение, – М.: Эдиториал УРСС, 2000. – 192 с.
5. Kalchenko V.I., Koshets I.A., Matsas E.P.,
Kopylov O.N., Solovyov A.V.,
Kazantseva Z.I., Shirshov Yu. M. Calixarene-based Acoustical Sensors Array And Its Response to Volatile Organic Vapours // Material Science. – 2002. –
Vol. 20,
№ 3. – P. 71-88.