Математика / 5. Математичне моделювання

Камаєва С.О.

Івано-Франківський національний технічний університет нафти і газу, Україна

Дослідження властивостей серендипових моделей

Відкриття серендипових елементів зробило великий крок в розвитку теорії методу скінченних елементів. Так, з обчислювальної точки зору ці елементи мають якісну перевагу над елементами лагранжевої сім’ї. Традиційно для їх побудови використовується апарат матричної алгебри, проте відомо, що перші моделі були знайдені підбором [1]. Наприклад, на біквадратичному елементі (рис. 1а) базисні функції стандартної моделі в типових вузлах мають вигляд [1]:

,

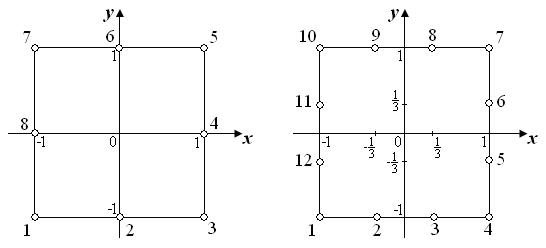
а) б)

Рис. 1 Біквадратичний (а) та бікубічний (б) серендипові елементи

Дослідимо дані функції на гармонічність.

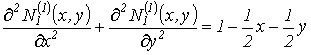
Так як ліва частина в загальному випадку не дорівнює нулю, то функція не є гармонічною за диференціальним критерієм Лапласа. А оскільки

,

то функція для проміжного вузла також не задовольняє даному критерію.

Проведемо дослідження цих функцій на гармонічність за інтегральними ознаками Кьобе та Привалова.

За Приваловим цей критерій в області круга формулюється так: якщо середнє значення по площі круга для функції співпадає із значенням в центрі круга, то функція є гармонічною за інтегральною ознакою.

В нашому випадку замість круга є квадрат розміром .

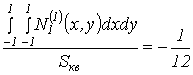, а значення в центрі квадрата .

З того, що 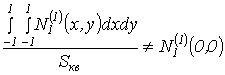, робимо висновок, що функція не є гармонічною за даним критерієм.

При дослідженні функції для проміжного вузла маємо:

, а .

Отже, ця функція також не є гармонічною за даним критерієм.

Значить, функції стандартного базису не витримують тестування на гармонічність за критерієм Привалова.

За Кьобе критерій гармонічності формулюється так: якщо середнє значення функції по контуру круга співпадає із значенням в центрі круга, то функція є гармонічною.

Середнє значення функції по контуру елемента рівне 1/12, що не співпадає із значенням в центрі –1/4. Середнє значення функції по контуру елемента рівне 1/6, а в центрі 1/2. Значить, функції стандартного базису не є гармонічними і за критерієм Кьобе.

Основним недоліком алгебраїчного підходу є те, що дана модель є єдиною і побудувати інші моделі з кращими характеристиками неможливо. Завдяки засобам геометричного моделювання крім стандартної моделі вдається отримати безліч альтернативних. Наведемо функції однієї з таких моделей в характерних вузлах [2]:

, .

Дослідження на гармонічність показало, що ці функції не задовольняють ні диференціальному, ні інтегральним критеріям. Однак, використовуючи процедуру «зважування» цих двох моделей

вдалось отримати модель, гармонічну за критерієм Привалова:

,

,

та модель, гармонічну за критерієм Кьобе:

,

На рис. 2 показано, який повузловий розподіл навантаження в стандартній моделі (а) та в моделях, гармонічних за ознаками Привалова (б) та Кьобе (в).

а) б) в)

Рис. 2 Повузловий розподіл рівномірної масової сили в наведених моделях

Аналогічні дослідження були проведені на бікубічному елементі (рис. 1 б). Виявилось, що стандартна модель

,

не задовольняє ні одному з критеріїв гармонічності.

При зважуванні даної моделі з альтернативною 16-параметричною моделлю [3]

,

вперше були отримані моделі, що містять 16 параметрів та є гармонічними за критерієм Привалова:

,

та критерієм Кьобе:

,

.

Таким чином, завдяки геометричному моделюванню та процедурі “зважування” існуючих моделей вдається отримати нові моделі з кращими властивостями.

ЛІТЕРАТУРА:

1. Зенкевич О. Метод конечных элементов в технике / О. Зенкевич. – М. : Мир, 1975. – 541 с.

2. Хомченко А.Н. Некласичний базис серендипового елемента з біквадратичною інтерполяцією / А. Н. Хомченко, С. О. Камаєва // Геометричне та комп’ютерне моделювання. – Харків: ХДУХТ, 2008. – Вип. 21. – С. 71-76.

3. Хомченко А. Н. Суперпараметрична модель бікубічної апроксимації / А. Н. Хомченко, С. О. Камаєва // Праці Таврійського державного агротехнологічного університету.– Том 42. – Мелітополь: ТДАТУ, 2009. – С. 33-38. – (Серія : Прикладна геометрія та інженерна графіка; вип. 4).