Д.ф.-м.н, проф. Горобец О. Ю ¹ , Васько Е. И.²

¹ Национальный технический университет Украины, Киев, Украина

² Донецкий национальный университет, Донецк, Украина

ПАРАМЕТРЫ ПОДОБИЯ ДВИЖЕНИЯ ЗАРЯЖЕННЫХ ЧАСТИЦ В ПОЛЯХ РАССЕЯНИЯ ПЛЁНКИ С ПОЛОСОВОЙ ДОМЕННОЙ СТРУКТУРОЙ

Управление заряженными частицами на микроскопическом уровне является актуальной задачей, для решения которой предлагается использовать изогнутые монокристаллы [1], системы нанокапилляров или сформированных за счёт поверхностного заряда участков поверхности [2, 3], управляющие магнитные поля [4]. В качестве управляющего элемента могут выступать тонкие магнитные плёнки с осью лёгкого намагничивания перпендикулярной их поверхности, содержащие регулярные доменные структуры (ДС). На перспективы их использования в данном аспекте указывают результаты численных экспериментов по рассеянию ионов и электронов [5 - 7]; показано, что заряженные частицы, движущиеся в полях рассеяния плёнок с полосовой ДС (ПДС), в зависимости от начальной ориентации можно рассеивать в режимах поверхностного каналирования, блокировки входа (рассеяние без столкновений с поверхностью плёнки), а также с однократными или многократными столкновениями частиц с её поверхностью. Цель работы – определение параметров подобия траекторий заряженных частиц, движущихся в поле рассеяния магнитной плёнки с ПДС.

Для выявления явной зависимости характера движения заряженных частиц в поле пленки с ПДС от основных параметров частиц и доменной структуры уравнение движения

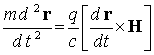(1)

записывается через безразмерный радиус-вектор , обезразмеренную напряженность магнитного поля пленки с ПДС и обезразмеренное время такими, что

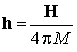, , , (2)

где – период ПДС, – напряжённость поля рассеяния ПДС, М – намагниченность плёнки, - некоторая постоянная размерности времени.

В результате имеем

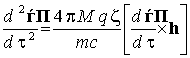, (3)

откуда

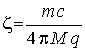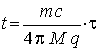и . (4)

Используя систему равенств

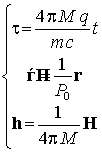, (5)

перейдем от (1) к обезразмеренному уравнению движения заряженных частиц в магнитном поле ПДС

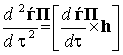. (6)

Выразив скорость частицы через безразмерные числа, получим:

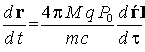, (7)

откуда видно, что подобие движения в поле рассеяния ПДС заряженных частиц должно иметь место, если выполняется .

Выразив компоненты поля рассеяния плёнки с ПДС [6, 7], через безразмерные числа и , уравнение движения запишется в виде

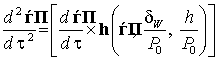. (8)

Видно, что если неизменно отношение толщины доменной стенки и ширины плёнки к периоду ПДС, то неизменна и функциональная зависимость , а, следовательно, и траектории движения заряженной частицы в поле рассеяния ПДС.

Т.о. в работе определены критерии подобия траекторий заряженных частиц, движущихся в поле рассеяния магнитной плёнки с ПДС.

Литература

[1] В.М. Бирюков, В.И. Котов, Ю.А. Чесноков. УФН 164, 1017 (1994).

[2] K.A. Vokhmyanina, L.A. Zhilyakov, A.V. Kostanovsky, V.S. Kulikauskas, V.P. Petukhov, G.P. Pokhil. Phys. A: Math. Gen 39, 4775 (2006).

[3] P. Skog, HQ. Zhang, and R. Schuch. Phys. Rev. Let 101, 223202 (2008).

[4] M. Schwabe, U. Konopka, P. Bandyopadhyay, and G. E. Morfill. Phys. Rev. Lett. 106, 215004 (2011).

[5] И.А. Мельничук, П.И. Мельничук. Мат. XV Междунар. конф. «Взаимодействие ионов с поверхностью». Тез. докл. М. (2001). С. 204.

[6] И.А. Мельничук, Е.И. Васько. Мат. XXXIX междунар. конф. по физике взаимодействия заряженных частиц с кристаллами. Тез. докл. М. (2009). С. 47.

[7] I.A. Melnichuk, E.I. Vasko, and S.V. Gavrilenko. Technical Physics 53, 1209 (2008).

[8] Е.И. Васько, П.И. Мельничук. Изв. РАН. Сер. физ. 68, 370 (2004).

[9] А.Л. Сукстанский, К.И. Примак. ФТТ 45, 105 (2003).