Веренич І.І., Ленюк М.П.

Буковинська державна фінансова академія

Чернівецький факультет НТУ «ХПІ»

Обчислення невласних інтегралів за власними елементами гібридного диференціального оператора Фур’є – Ейлера на декартовій вісі

Побудуємо обмежений на множині розв’язок сепаратної системи звичайних диференціальних рівнянь другого порядку Фур’є та Ейлера для модифікованих функцій

(1)

за умовами спряження

(2)

У рівностях (1), (2) - диференціальний оператор Ейлера [1].

Фундаментальну систему розв’язків для диференціального рівняння Фур’є утворюють функції та (або їх лінійні комбінації та ) [1]; фундаментальну систему розв’язків для диференціального рівняння Ейлера утворюють функції та [1].

Наявність фундаментальної системи розв’язків дозволяє будувати розв’язок крайової задачі (1), (2) методом функцій Коші [1,2]:

(3)

Тут - функції Коші [1,2]:

(4)

де

Введемо до розгляду функції:

Безпосередньо перевіряється, що за функції Коші можуть служити функції:

(5)

(6)

Умови спряження (2) для визначення величин дають алгебраїчну систему рівнянь:

(7)

У системі (7) бере участь функція

Припустимо, що виконана умова однозначної розв’язності даної крайової задачі: для будь-якого ненульового вектора визначник алгебраїчної системи (7) відмінний від нуля:

(8)

У результаті однозначної розв’язності алгебраїчної системи (7), підстановки одержаних значень та у формули (3) одержуємо єдиний розв’язок крайової задачі (1), (2) :

(9)

У рівностях (9) беруть участь головні розв’язки даної крайової задачі:

1) породжені неоднорідністю системи функції впливу

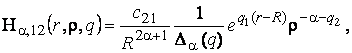
(10)

2) породжені неоднорідністю умов спряження функції Гріна

(11)

Побудуємо розв’язок крайової задачі (1), (2) методом гібридного інтегрального перетворення, породженого на множені гібридним диференціальним оператором (ГДО)

(12)

- одинична функція Гевісайда [2].

Оператор самоспряжений й має дві особливі точки та . У цьому випадку спектр оператора неперервний, а спектральна функція комплексно спряжена [3].

Фундаментальний розв’язок для диференціального рівняння Фур’є утворюють функції та [1]; фундаментальний розв’язок для диференціального рівняння Ейлера утворюють функції та [1]. Тут - спектральний параметр.

Визначимо функції:

Безпосередньо перевіряється, що функції

(13)

де , задовольняють відповідно диференціальні рівняння та однорідні умови спряження

Отже, спектральна функція ГДО

Наявність спектральної функції вагової функції де та спектральної густини дає можливість запровадити породжене на множині ГДО гібридне інтегральне перетворення Фур’є – Ейлера [3]:

(14)

(15)

(16)

Припустимо, що Покладемо ,

Побудований методом гібридного інтегрального перетворення, запровадженого формулами (14) – (16), єдиний розв’язок крайової задачі (1), (2) описують функції:

(17)

Порівнюючи в силу єдиності розв’язки (9) та (17), одержуємо формули обчислення таких поліпараметричних невласних інтегралів:

(18)

(19)

(20)

Оскільки функції впливу та функції Гріна не залежать від нерівності або нерівності (у випадку ), то можна покласти , звужуючи при цьому сім’ю невласних інтегралів.

З викладеного вище випливає твердження.

Основна теорема. Якщо вектор-функція неперервна на множинні , функції задовольняють умови спряження (2) та виконується умова (8) однозначної розв’язності крайової задачі (1), (2), то справджуються формули (18) – (20) обчислення поліпараметричних невласних інтегралів за власними елементами ГДО , визначеного рівністю (12).

1. Степанов В.В. Курс дифференциальных уравнений. – М.: Физматгиз, 1959. – 468 с.

2. Шилов Г.Е. Математический анализ. Второй специальный курс. – М.: Наука, 1965. – 328 с.

3. Ленюк М.П., Шинкарик М.І. Гібридні інтегральні перетворення (Фур’є, Бесселя, Лежандра). Частина 1. – Тернопіль: Економічна думка, 2004. – 368 с.